الجذ ور المربعة

جذر مربع a

أمثلة
$\sqrt{4}$ يمثل العددالموجب مربعه 2: العدد هو: $\sqrt{4}=2$
$\sqrt{9}$ يمثل العددالموجب مربعه 9:العدد هو: $\sqrt{9}=3$
التعريف.
جذر مربع العدد a هو العدد الذي مربعه a
${\color{Red} r=\sqrt{a}}$

خاصية:

مهما كان a عددا حقيقيا موجبا فإن:

أمثلة

العمليات على الجذور المربعة

جمع وطرح على الجذور المربعة

الأمثلة

1) لنحسب

لدينا

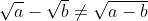
نلا حظ ان $\sqrt{a}\ +\sqrt{b}\neq \sqrt{a+b}$

2 ) لنحسب

لدينا

نلاحظ ان $\sqrt{a^{2}+b^{2}}\neq a+b$

3) لنحسب

لدينا

نقول ان $\sqrt{a}-\sqrt{b}\neq \sqrt{a-b}$

نستنتج :

بصفة عامة لا توجد صيغة او قاعدة مع الجمع والطرح للأ عداد الجذرية

الجذر المربع و الجداء

خاصية

جداء عددين جذ ريين هو جذر مربع لجداء العددين

برهان
ملا حظة

لكل

بصفة عامة فان الجذر المربع للعدد a يساوي القيمة المطلقة ل a : $\sqrt{a^{2}}=\left | a \right |$
امثلة
احسب $\sqrt{5}\ \times\sqrt{3}$
$\sqrt{5}\ \times\sqrt{3} =\sqrt{5\times 3}=\sqrt{15}$
بسيط $\sqrt{80}$

احسب $\sqrt{12}\ \times \sqrt{3}$
$\sqrt{12}\ \times \sqrt{3}=\sqrt{12\times 3}=\sqrt{36}=\sqrt{6^{2}}=6$
استنتاج
لكل

الجذر المربع و الخارج:

خاصية :

الخارج لعددين جذريين هو جذ ر لخارج العددين

برهان

مثال

احسب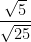 $\frac{\sqrt{5}}{\sqrt{25}}$

$\frac{\sqrt{5}}{\sqrt{25}}=\sqrt{\frac{5}{25}}=\sqrt{\frac{1}{5}}=\frac{ \sqrt{1}}{\sqrt{5}}=\frac{\sqrt{5}}{5}$ او $\frac{\sqrt{5}}{\sqrt{25}}=\frac{ \sqrt{5}}{\sqrt{5^{2}}}=\frac{\sqrt{5}}{5}$

حدف الجذر المربع من المقام :

لحساب القيم التقريبية بسهولة ، من الأفضل أن يكون هناك جذر في البسط من المقام لهذا نستعمل خاصية 1 او خاصية 2

خاصية 1 :

خاصية 2 :

امثلة:

1 ) لنحدف الجذر المربع من المقام: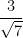 $\frac{3}{\sqrt{7}}$

$\frac{3}{\sqrt{7}}=\frac{3\times \sqrt{7}}{\sqrt{7\ \times \sqrt{7}}}=\frac{3\sqrt{7}}{\sqrt{7}^{2}}=\frac{3\sqrt{7}}{7}$

لنحدف الجذر المربع من المقام : $\frac{2+\sqrt{3}}{3\sqrt{5}}$
$\frac{2+\sqrt{3}}{3\sqrt{5}}=\frac{(2+\sqrt{3})\times \sqrt{5}}{3\sqrt{5}\times \sqrt{5}}=\frac{(2+\sqrt{3})\times \sqrt{5}}{3\sqrt{5}^{2}}=\frac{2\sqrt{5}+\sqrt{3}\sqrt{5} }{3\ \times 5}=\frac{2\sqrt{5}+\sqrt{15}}{15}$

3 ) لنحدف الجذر المربع من المقام باستعمال المرافق:
مثال 1 : $\frac{3}{\sqrt{5}\ -1}$ مرافق العددادن $\frac{3}{\sqrt{5}\ -1}=\frac{3\ \times(\sqrt{5}\ +1) }{(\sqrt{5}\ -1)\times (\sqrt{5}\ +1)}=\frac{3\ \times (\sqrt{5}+1)}{\sqrt{5}^{2}\ -1^{2}}=\frac{3\sqrt{5}+3}{5-1}=\frac{3\sqrt{5}+3}{4}$
مثال 2 : $\frac{4}{2+\sqrt{2}}$ مرافق العدد ادن $\frac{4}{2+\sqrt{2}}=\frac{4\times (2-\sqrt{2})}{(2+\sqrt{2)}\times (2-\sqrt{2})}=\frac{8-4\sqrt{2}}{2^{2}-\sqrt{2}^{2}}\\\ \ \\ =\frac{8-4\sqrt{2}}{4-2}=\frac{2\times (4-2\sqrt{2})}{2}=4-2\sqrt{2}$

حل المعادلة ${\color{Red} x^{2}=a}$

قاعدة:

مثال:
حل المعادلة: ${\color{Red} x^{2}-16=0}$
${ x^{2}-16=0$ يعني ${ x^{2}=16$ اذن   $x=\sqrt{16}=4\ او\ x= -\sqrt{16}=-4$ او $x= -\sqrt{16}=-4$
بصيغة اخرى ${ x^{2}-16=0$ يعني $x^{2}=16$ اي $x^{2}=4^{2}$ بمعنى   $x=4$ او   $x=-4$
المعادلة ${\color{Red} x^{2}-16=0}$ لها حلين هما ${\color{red} x_{1}=4}$ و   ${\color{red} x_{2}=-4}$

الرياضيات

القائمة الرئيسية

الصفحات

الجذ ور المربعة

Commentaires

Enregistrer un commentaire