القائمة الرئيسية

الصفحات

تعديل المشاركة

nombres complexes

has
(0)

1)Ensembles des nombres complexes
2) forme algébrique d 'un nombre complexe (vidéo)
3) Le conjugué  et  inverse d 'un nombre complexe 
4) Résultats directs et propriétés (vidéo)
5) Module d’un nombre complexe :(vidéo)
6 )distance entre deux points  du   plan complexe (vidéo)
7 )l 'ensemble U
8) Forme trigonométrique d'un nombre complexe
1)Ensembles des nombres complexes
Définition 
On admet qu'il existe  un ensemble des nombres qu'on note https://mathshas.blogspot.com/  : c'est l'ensemble des nombres complexes , vérifiant les propriétés suivantes :
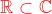
1)  {\color{Red} \mathbb{R}}{\color{Red}\ \subset \mathbb{C}}
2) {\color{Red} \mathbb{C}} contient un nombre i tel que i² =  - 1
3) tous les éléments de {\color{Red} \mathbb{C}}  s'écrivent sous forme  a + i b avec  a ∈ ℝ et b ∈ℝ
4) L'ensemble https://mathshas.blogspot.com/ des nombres complexes est une extension de l'ensemble ℝ et les règles de calcul des quatre opérations  + ; - ; × et  ÷ sont conservées
Exemples  :  2 i  ; 5   ;  √3  ;  i √5 ; 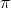 \pihttps://mathshas.blogspot.com/ ;  9  sont des nombres complexes 
2) forme algébrique d 'un nombre complexe (vidéo) ((:
(∀ z ∈ https://mathshas.blogspot.com/ )  ( ∃ ! (a ; b) ∈ ℝ²  :  z = a + i b 
a + i b est la forme algébrique   de nombre complexe z 
a : c'est la partie réelle de z  ,  notée  Re (z)
b : c'est la partie imaginaire de z , notée Im(z)
Remarque :
z ∈ ℝ signifie que Im (z) = 0 
z ∉ ℝ  signifie que  Im(z) ≠ 0
Si  Re (z) = 0 alors  z = i b  on dit que  z est un nombre imaginaire pur et par suite l'ensemble des imaginaires purs est l 'ensemble  i ℝ = { i b /  b ∈ ℝ } donc
 z ∈ i ℝ ⇔ Re(z) =0   et  i ℝ  ∩ ℝ = 0
Exercices d 'applications :
Ecrire les nombres complexes sous forme algébrique:



3) Le conjugué  et  inverse d 'un nombre complexe 

Définition :
Soient ( a ; b ) ∈ ℝ²  et z = a + i b  un nombre complexe  , on appelle  conjugué  de z = a+ i b le  nombre complexe 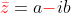 {\color{red} \bar{z}}= a{\color{Red} -}ib
Remarques :
∀  (a ; b) ∈ ℝ²  : a² + b² = ( a + i b ) ( a - i b )
l 'opposé du nombre complexe  z = a + i b est  z =  - a - i b ≠ 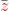 \bar{{\color{Red} z}}
Proposition : l inverse  d'un nombre complexe   non nul  z = a + i b  est le  nombre complexe  \frac{1}{z}=z^{-1}=\frac{1}{a+ib}=\frac{a}{a^{2}+b^{2}}-i\frac{b}{a^{2}+b^{2}}
4) Résultats directs et propriétés 
Soient  z et 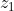z_{1} deux nombres complexes
5) Module d’un nombre complexe :(vidéo)
5.1)Définition:

Soit z un nombre complexe
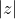
Le nombre réel   est le module de z on le note \left|z\right|

Remarques :
 est un nombre réel 
Si z∈ ℝ donc le module de z est la valeur absolue de z 

Interprétation  graphique :
Soit z = a + i b  un nombre complexe et M son image dans un repère complexe
 le module  de z est la distance OM



5.2) propriétés:
Soient z et z' deux complexes  : |z.z'| =|z| .|z'|   


Re(z) ≤ |Re(z)| ≤ | z | et Im(z) ≤ | Im(z)| ≤ | z |

| z + z' | ≤ | z | + | z' | 
6 )distance entre deux points  du   plan complexe (vidéo)
soient A  et  B deux points distincts d' affixes respectives 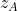 z_A  et   z_B  du plan complexe 

La distance entre A et B  est le module de   


Démonstration:
  Exemples:
   et  deux complexes  ; A  et  B deux points distincts d' affixes respectives z_A et  z_B
calculons  distance  entre  A et B

Quelle est la distance entre le point A d’affixe  et  le point B d’affixe dans le plan complexe ?
Représentant les point A(z_A )et B(z_B) sur le plan complexe : le point A à pour coordonnées ( 5; 3) et le point B à pour coordonnées ( -3 ; -1)

Calcul de la distance ( longueur) AB
 et comme 
donc 
calcul de la distance AB    utilisant  Théorème de Pythagore:
 on trace Le triangle rectangle ABC .Puis  calculant la longueur de L'hypoténuse AB
7 )l 'ensemble U
L'ensemble U est l'ensemble des nombres complexes dont le module est égale à 1 on le note U = { z ∈ ℂ / | z| = 1}  
7-1) propriétés:
(∀ z ∈ U ) :  z ≠ 0             ;  (∀ z ∈ U ) : 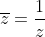\overline{z}=\frac{1}{z}       
    (∀ z ∈ U ) : 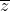 \overline{z}∈ U et    (﹣ z )∈ U    
  ∀ ( z ; z' )∈  U² :  (z ×  z') ∈ U  
∀ ( z ; z' )∈  U² :  
L'image de U dans le plan complexe est un cercle trigonométrique 
 
preuve:

8) Forme trigonométrique d'un nombre complexe
8-1) Argument d'un nombre complexe 
Définition :
(∀ z ∈ U) (∃ θ ∈ ℝ)  : z = cosθ   + i sinθ    ;  le nombre réel θ  est  appelé argument de nombre complexe z on le note arg(z)
Conséquence: (∀ z ∈ ℂ*)  ( ∃ θ' ∈ ℝ) : z = |z| (cos θ'  + i sinθ')  ; θ' est aussi argument de z  est noté arg(z)    avec θ' ≡ arg( z/|z|)  [2π]
l'écriture : z = z = |z| (cos θ'  + i sinθ') est la forme trigonométrique de nombre complexe z ; noté  z = [ |z| ;  θ' ]
Exemple:
Soit le complexe   
Remarque:
Argument M (z ) est la mesure de l 'angle 
Si θ est argument de z ,alors tous nombre  de forme ( θ +2kπ ,avec k∈ℤ ) est argument de z
8-2) Relation entre les coordonnées polaires et cartésiennes
 Dans l'espace muni d'un repère cartésien  tout point M pour coordonnées (x ; y ; z) signifie que M est déterminé par :
Dans le plan muni d'un repère orthonormé direct   La longueur du segment OM = r  La longueur du segment  correspond à la coordonnée radiale r
L'angle θ est la coordonnée angulaire. Cet angle est mesuré par rapport à l'axe des abscisses ox .
Les coordonnées polaires du point M sont : ( r ;θ )
Les composantes du vecteur positionsont : (r ; o ) 

Soit z ∈ ℂ*   si z = x + i y   ( x  ; y )∈ ℝ² avec  x≠ 0  et y ≠ 0   et argument de z = θ

هل اعجبك الموضوع :

أخر المواضيع من قسم : 2ème année bac

Commentaires

Enregistrer un commentaire