Ordre dans \(\mathbb{R}\)
Définition :
Soient \(a\) et \(b\) deux réels.
1) on dit que \(a\) est supérieur ou égale à \(b\) qu 'on note \(a\ge b\) si \(a-b\) est positif
2) on dit que \(a\) est inférieur ou égale à \(b\) qui ' on note \(a\le b\) si \(a-b\) est négatif
Exemples
Comparer nombres suivant: \(x=2 \ et\ y=\frac{5}{2}\)

Soit \(n\) un nombre entier naturel différent de zéro (\(n ∈ \mathbb{N} .; n ≠ 0\) ) comparer :
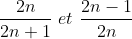
Soit \(n\) un nombre entier naturel différent de zéro (\(n ∈ \mathbb{N} .; n ≠ 0\) ) comparer :
\(n ∈ \mathbb{N}^* \ alors\ n\gt0 \ et\ 1\gt0 \rightarrow \ 2n+1\gt0\)
donc
\(2n(2n+1)\gt0\)
Calculons :
\(\frac{2n}{2n+1}-\frac{2n-1}{2n}\)
\(\frac{2n}{2n+1}-\frac{2n-1}{2n}=\frac{(2n)^{2}-(2n)^{2}+1}{2n(2n+1)}=\frac{1}{2n(2n+1)}\gt 0\)
\(\frac{2n}{2n+1}\gt \frac{2n-1}{2n}\)
Ordre et opérations :
Propriétés:
soient a, b , c et d des nombres réels
1) si a ≤ b alors a +c ≤ b +c autrement: ajouter ou soustraire un même nombre aux deux membres d' une inégalité conserve l'ordre
2) si a ≤ b et c ≤ d alors a + c ≤ b +d ( encadrement d 'une somme)
3) Multiplier chaque membre de l'inégalité:
* par un même nombre strictement positif ne change pas le sens de l'inégalité
* par un même nombre strictement négatif change le sens de l inégalité
si a ≤ b et c ≥ 0 alors ac ≤ b c
si a ≤ b et c ≤ 0 alors ac ≥ b c
4) Diviser chaque membre de l'inégalité:
* Par un même nombre strictement positif ne change pas le sens de l'inégalité
* Par un même nombre strictement négatif change le sens de l'inégalité
Si ac ≤ b c et c > 0 alors a ≤ b
Si ac ≤ b c et c < 0 alors a ≥ b
Si \(a\le b \quad et\quad c\gt 0\quad alors\quad\frac{a}{c}\le \frac{b}{c}\)
Si \(a\le b \quad et\quad c\lt 0\quad alors\quad\frac{a}{c}\ge \frac{b}{c}\)
Si 0 ≤ a ≤ b et 0 ≤ c ≤ d alors ac ≥ b d
Si \( bd\gt 0 \quad et\quad \frac{a}{b}\lt \frac{c}{d}\quad alors\quad ad\lt bc\)
Exemples:
1/ 1 ≤ 3 donc 1 + 2 ≤ 3+ 2
2/ si x ≤ - 2 et y ≤ 6 donc x + y ≤ - 2 + 6 = 4
3/ \(x\le \frac{5}{2}\) et \(2\gt 0\) donc \(2x\le 2\times \frac{5}{2}\) donc \(\ 2x\le 5\)
4/\(x\lt \frac{3}{2}\) et \(-2\lt 0\) donc \( (-2)x\gt (-2)\times \frac{3}{2}\) donc\( -2x\gt 3\)
5/ \(5x\le 7\) donc \(\frac{1}{5}\times 5x\le \frac{1}{5}\times 7\) car \(\frac{1}{5}\gt 0\) donc \(x\le \frac{7}{5}\)
6) Si (0 ≤ x ≤ 2) et (0 ≤ y ≤4) alors (x y ≤ 2 × 4) c'est à dire (x y ≤ 8)
7) Si 0 ≤ 2 x ≤ 8 et 0 ≤ 5 y ≤ 10 montrons que x y ≤ 8
Ordre et inverse
Propriétés :
Soient a et b deux réels non nul
\[\begin{cases} 0\leq2x\leq8\Rightarrow 0\leq x\leq4\leq y \\ \\ 0\leq5y\leq10\Rightarrow 0\leq y\leq2\end{cases}\quad signifie \ que\ xy\le 8\]
Ordre et inverse
Propriétés :
Si \(\quad 0\lt a\le b\quad alors\quad 0\lt \frac{1}{b} \le \frac{1}{a}\)
Si \(a\le b\lt 0\quad alors \quad\frac{1}{b}\le \frac{1}{a}\lt 0\)
Exemples :
1) \( 0\lt x\le 6\quad alors \quad 0\lt \frac{1}{6} \le \frac{1}{x}\)
2) \(3\lt 4 \quad alors\quad \frac{1}{4} \lt \frac{1}{3}\)
3) \(\frac{1}{5}\lt \frac{1}{7} \quad donc\quad 7\gt 5\)
4) Soit
\(x\in \mathbb{R}\quad avec\quad x\neq(\frac{-1}{4}) \quad tel\ que \quad 0\lt \frac{2}{4x+1}\lt \frac{2}{3}\)
Montrer que:
\(x\gt \frac{1}{12}\)
Comme donné on a
\(0\lt \frac{2}{4x+1}\lt \frac{3}{2}\) multipliant chaque membre de l'inégalité par \(2(4x+1)\) on obtient \(0\lt \frac{4(2x+1)}{4x+1}\lt \frac{2\times 3(4x+1))}{2}\)
ce qui donne \(0\lt 4\lt 12x+3\) ajoutant ( -3) aux membres de l'inégalité \(\Rightarrow -3\lt 1\lt 12x \) on dise par 12 ce qui donne \(\frac{-1}{4}\lt \frac{1}{12}\lt x \) D’où \(\frac{1}{12}\lt x\) donc \(x\gt \frac{1}{12}\)
comparer les nombres
\(\frac{1}{3^{2045}-3145} et \frac{1}{3^{2045}-2564}\)
On sait que \((-3145)\lt (-2564)\) si on ajoute le nombre \(3^{2045}\) qui est positif à l' inégalité : l'inégalité est inchangeable on aura \(3^{2045}-3145\lt 3^{2045}-2564\)
Donc
\(\frac{1}{3^{2045}-2564} \gt \frac{1}{3^{2045}-3145}\)
الترتيب في المجموعة\(\mathbb{R}\)
التعريف:
لنعتبر \(a\) و \(b\) عددين حقيقيين.
1) نقول أن \(a\) أكبر من أو يساوي \(b\)، الذي نرمز له بـ \(a \ge b\)، إذا كان \(a - b\) عددًا موجبًا.
2) نقول أن \(a\) أصغر من أو يساوي \(b\)، الذي نرمز له بـ \(a \le b\)، إذا كان \(a - b\) عددًا سالبًا.
أمثلة:
قارن بين العددين التاليين: \(x = 2\) و \(y = \frac{5}{2}\).
نحسب \(x - y = 2 - \frac{5}{2} = \frac{4 - 5}{2} = \frac{-1}{2} < 0\)، لذا \(x < y\).
مسألة:
لنأخذ \(n\) عددًا صحيحًا طبيعيًا غير صفر (\(n \in \mathbb{N}^*\)، حيث \(n \neq 0\))، قارن بين:
إذا كان \(n \in \mathbb{N}^*\) فإن \(n > 0\) و \(1 > 0 \rightarrow 2n + 1 > 0\)، وبالتالي \(2n(2n + 1) > 0\).
حساب:
\[\frac{2n}{2n + 1} - \frac{2n - 1}{2n}\]
المقام المشترك هو \(2n(2n + 1)\)، لذا نكتب:
\[\frac{2n(2n + 1)}{2n(2n + 1)} = \frac{2n(2n + 1)}{2n(2n + 1)}\]
ملاحظة:
مقارنة بين عددين حقيقيين \(a\) و \(b\) تعني دراسة إشارة الفرق بينهما، أي \(a - b\).
الترتيب والعمليات:
الخصائص:
لنعتبر \(a\)، \(b\)، \(c\) و \(d\) أعدادًا حقيقية.
1) إذا كان \(a \le b\)، فإن \(a + c \le b + c\). بمعنى آخر، إضافة أو طرح نفس العدد من طرفي المتباينة يحافظ على ترتيب الأعداد.
2) إذا كان \(a \le b\) و \(c \le d\)، فإن \(a + c \le b + d\) (أي تربيع الحدين معًا).
3) ضرب كل طرف من المتباينة:
- إذا ضربنا كلا الطرفين في نفس العدد الموجب، فإن الاتجاه لا يتغير.
- إذا ضربنا كلا الطرفين في نفس العدد السالب، فإن الاتجاه يتغير.
إذا كان \(a \le b\) و \(c \ge 0\)، فإن \(ac \le bc\).
إذا كان \(a \le b\) و \(c \le 0\)، فإن \(ac \ge bc\).
4) قسمة كل طرف من المتباينة:
- إذا قسمنا كل طرف على نفس العدد الموجب، فإن الاتجاه لا يتغير.
- إذا قسمنا كل طرف على نفس العدد السالب، فإن الاتجاه يتغير.
إذا كان:
\(ac \le bc\) و \(c > 0\)، فإن \(a \le b\).
\(ac \le bc\) و \(c < 0\)، فإن \(a \ge b\).
إذا كان:
\(a \le b\) و \(c > 0\)، فإن \(\frac{a}{c} \le \frac{b}{c}\)
\(a \le b\) و \(c < 0\)، فإن \(\frac{a}{c} \ge \frac{b}{c}\)
إذا كان:
\(0 \le a \le b\) و \(0 \le c \le d\)، فإن \(ac \ge bd\)
إذا كان:
\(bd > 0\) و \(\frac{a}{b} < \frac{c}{d}\)، فإن \(ad < bc\)
أمثلة:
1) إذا كان \(1 \le 3\)، فإن \(1 + 2 \le 3 + 2\).
2) إذا كان \(x \le -2\) و \(y \le 6\)، فإن \(x + y \le -2 + 6 = 4\).
3) إذا كان \(0 \le x \le 2\) و \(0 \le y \le 4\)، فإن \(xy \le 2 \times 4\)، أي \(xy \le 8\).
4) إذا كان \(0 \le 2x \le 8\) و \(0 \le 5y \le 10\)، أظهر أن \(xy \le 8\).
الترتيب والعكس
الخصائص:
لنعتبر \(a\) و \(b\) عددين حقيقيين.
إذا كان \(\quad 0 < a \le b\)، فإن \(\quad 0 < \frac{1}{b} \le \frac{1}{a}\)
إذا كان \(\quad a \le b < 0\)، فإن \(\quad \frac{1}{b} \le \frac{1}{a} < 0\)
أمثلة:
1) إذا كان \( 0 < x \le 6\)، فإن \(\quad 0 < \frac{1}{6} \le \frac{1}{x}\).
2) إذا كان \(3 < 4\)، فإن \(\quad \frac{1}{4} < \frac{1}{3}\).
3) إذا كان \(\frac{1}{5} < \frac{1}{7}\)، فإن \(\quad 7 > 5\).
4) إذا كان \(x \in \mathbb{R}\) و \(x \neq \frac{-1}{4}\) و إذا كان \(0 < \frac{2}{4x+1} < \frac{3}{2}\)، أظهر أن \(x > \frac{1}{12}\).
نظرًا لما هو معطى، لدينا \(0 < \frac{2}{4x+1} < \frac{3}{2}\). من خلال ضرب كل طرف من المتباينة في \(2(4x+1)\)، نحصل على:
\[0 < \frac{4(2x+1)}{4x+1} < \frac{2 \times 3(4x+1)}{2}\]
هذا يعطي:
\[0 < 4 < 12x + 3\]
من خلال إضافة \(-3\) إلى كلا الطرفين:
\[-3 < 1 < 12x\]
ثم قسمنا على 12، فنحصل على:
\[\frac{-1}{4} < \frac{1}{12} < x\]
إذن، \(x > \frac{1}{12}\)
2) قارن بين العددين \(\frac{1}{3^{2045} - 3145}\) و \(\frac{1}{3^{2045} - 2564}\).
نعرف أن \(-3145 < -2564\)، وإذا أضفنا العدد \(3^{2045}\) الذي هو عدد موجب إلى المتباينة، فلن يتغير اتجاه المتباينة، وبالتالي:
\[3^{2045} - 3145 < 3^{2045} - 2564\]
لذا:
\[\frac{1}{3^{2045} - 2564} > \frac{1}{3^{2045} - 3145}\]

Commentaires
Enregistrer un commentaire