Exercices Équations du second degré

cours et Énoncé d' exercices ici

Exercice 1

résolution d'équations

x² - 6 x + 8 = 0 Δ = (- 6)² - 4 × 8 = 36 - 32 = 4

Δ > 0 donc l 'équation x² - 6 x + 8 = 0 admet deux solutions dans ℝ ${\color{Red} x_{1}}= \frac{6-\sqrt{\Delta}}{2}=\frac{6-2}{2}={\color{Red} 2}\ et\ {\color{Red} x_{2}}=\frac{6+2}{2}={\color{Red} 4}$ donc S={2 ; 4}

x² + x +1 = 0 Δ = 1 - 4 = - 3

Δ < 0 donc l'équation x² + x +1 = 0 n'admet pas de solution dans ℝ donc S= ∅

$\bg_green {\color{Red} 9 x^{2} + 2 x + \frac{1}{9} = 0 }$ Δ = (2)² - 4 × 9 × 1/9 = 4 - 4 = 0

Δ = 0 donc l 'équation admet une solution unique dans ℝ 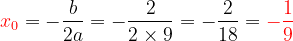${\color{Red} x_{0}}=-\frac{b}{2a}=-\frac{2}{2\times 9}=-\frac{2}{18}={\color{Red} -\frac{1}{9}}$

donc 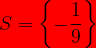$\bg_red S=\left \{- \frac{1}{9} \right \}$

$\large {\color{Red} -2x^{2}+x+1=0}$ Δ = 1 - (4 × (- 2)) = 9

Δ > 0 donc l 'équation -2 x² + x + 1 = 0 admet deux solutions dans ℝ

${\color{Red} x_{1}}= \frac{-1-\sqrt{\Delta}}{-2\times 2}=\frac{-1-3}{-4}={\color{Red}1}\ et\ {\color{Red} x_{2}}=\frac{-1+\sqrt{\Delta}}{-2\times 2}=\frac{-1+3}{-4}={\color{Red} \frac{-1}{2}}$

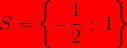
donc $\bg_red S=\left \{- \frac{1}{2}\ ;\ 1 \right \}$

Exercice 2

factorisation des polynômes

$P(x) = 4 x^{2} +5 x + 1$ Δ = b² - 4 a c = 25 - 16 = 9

9 > 0 donc $\bg_red P(x) =4(x-{\color{White} x_{1}})(x-{\color{White} x_{2}})$ avec ${\color{Red} x_{1}}= \frac{-5-\sqrt{\Delta}}{2\times 4}=\frac{-5-3}{8}={\color{Red}-1}\ et\ {\color{Red} x_{2}}=\frac{-5+\sqrt{\Delta}}{2\times 4}=\frac{-5+3}{8}={\color{Red} \frac{-1}{4}}$

$\bg_red P(x) =4(x+{\color{White} 1})(x+{\color{White} \frac{1}{4}})$

$\bg_blue {\color{White} Q(x) = x^{2} + 12 x + 11}$ Δ = b² - 4 a c = 144 - 44 = 100

Δ = 100 > 0 donc ${\color{Blue} Q(x) = (x-{\color{Red} x_{1}})(x-{\color{Red} x_{2}})}$ avec

${\color{Red} x_{1}}= \frac{-12-\sqrt{\Delta}}{2}=\frac{-12-10}{2}={\color{Red}-11} \\ {\color{Red} x_{2}}=\frac{-12+\sqrt{\Delta}}{2}=\frac{-12+10}{2}={\color{Red} -1} d' o\grave{u}\ {\color{Blue} Q(x)=(x+ {\color{Red} 11})(x+ {\color{Red} 1})}$

$H(x) = x^{2} - 5 x + 4$ Δ = 25 - 16 =9 > 0 donc $\bg_green H(x) = \left (x- {\color{Red} x_{1}} \right )\left ( x-{\color{Red} x_{2}} \right )$

tel que :

${\color{Red} x_{1}}=\frac{5-3}{2}={\color{Red}1} \\ {\color{Red} x_{2}}=\frac{5+3}{2}={\color{Red}4} \ \ d' o\grave{u}$ $\bg_green H(x) = \left (x- {\color{Red} 1} \right )\left ( x-{\color{Red}4} \right )$

$L(x)=x^{2} +5x -\frac{49}{4}$ $\Delta = 25 - 4\left ( \frac{-49}{4} \right )=25+49=74> 0$ donc

$\bg_blue L(x)=\left (x -{\color{DarkOrange} x_{1}} \right )\left ( x-{\color{DarkOrange} x_{2}} \right )$ $avec \ {\color{Red} x_{1}}=\frac{-5-\sqrt{74}}{2}\ et\ {\color{Red} x_{2}}\frac{-5+\sqrt{74}}{2}$

$\bg_blue L(x)=\left (x -{\color{DarkOrange} \left ( \frac{-5-\sqrt{74}}{2} \right )} \right )\left ( x-{\color{DarkOrange} \left ( \frac{-5+\sqrt{74}}{2} \right )} \right )$

Exercice 3

a et b deux racines de l équation 4 x² - 7 x - 1 = 0

1)calcul de a et b

$\Delta = 7^{2}- 4\times \left (-1 \right )\times 4=49+16=65\\ a=\frac{7-\sqrt{65}}{2\times 4}=\frac{7-\sqrt{65}}{8}\\\\ b= \frac{7+\sqrt{65}}{2\times 4}=\frac{7+\sqrt{65}}{8}\\ \\ a+b= \frac{7-\sqrt{65}}{8}+ \frac{7+\sqrt{65}}{8}=\frac{14}{8}=\frac{7}{4}\ \\ \\ \\ \ ab=\left ( \frac{7-\sqrt{65}}{8} \right )\left (\frac{7+\sqrt{65}}{8} \right )=\frac{49}{64}-\frac{65}{64}=-\frac{16}{64}=-\frac{1}{4}\\ \\ \\ a^{2}+b^{2}= a +b -2ab +2ab = (a+b)^{2}-2ab=\frac{7}{4}-2\times (-\frac{1}{4})=\frac{9}{4}$

$a^{2}+b^{2}= a +b -2ab +2ab = (a+b)^{2}-2ab=\frac{7}{4}-2\times (-\frac{1}{4})=\frac{9}{4}\\ \\ \frac{1}{a^{2}}+\frac{1}{b^{2}}=\frac{a^{2}+b^{2}}{(ab)^{2}}=\frac{\frac{9}{4}}{\frac{1}{16}}=\frac{9}{4}\times 16=36\\ \\ a^{4}+b^{4}=\left ( a+b \right )^{4}-\left ( 4a^{3}b +6a^{2}b^{2}+4ab^{3}\right )=(a+b)^{4}-2ab(2a^{2}+3ab+2b^{2})\\ \\ =\left ( \frac{7}{4} \right )^{2}-2\left ( -\frac{1}{4} \right )\left ( 2\times \frac{9}{4} +3\left ( -\frac{1}{4} \right )\right )=\frac{2401}{256}+\frac{2}{4}\times \frac{15}{4}=\frac{2401+480}{256}=\frac{2881}{256}$

exercice 4

Exercice 5

Résoudre dans ℝ les systèmes suivants

$\begin{cases}x+y = 8 \\xy=12 \end{cases}\ \ ;\ \ \begin{cases}x^{2}+y^{2} = 98 \\xy=15 \end{cases}$

$\begin{cases}x^{2}+y^{2} = 98 \\xy=15 \end{cases}$
$\large \bg_white \begin{cases}x^{2}+y^{2} = 98 \\xy=15 \end{cases}\Leftrightarrow \begin{cases}(x+y)^{2} -2xy= 98 \\xy=15 \end{cases}\Leftrightarrow \begin{cases}(x+y)^{2} -30= 98 \\xy=15 \end{cases}\\ \\ \Leftrightarrow \begin{cases}(x+y)^{2} = 128 \\xy=15 \end{cases}\Leftrightarrow \begin{cases}(x+y)^{2} = 8\sqrt{2} \\xy=15 \end{cases}\ \ ou\ \begin{cases}(x+y)^{2} = -8\sqrt{2} \\xy=15 \end{cases}$

$donc \ revient\ \grave{a}\ r\acute{e}soudre\ les \ \acute{e}quations\\ x^{2}-8\sqrt{2}\ x+15=0\\ x^{2}+8\sqrt{2}\ x+15=0\\ on\ a\: \Delta=128-60=68\\ \\ x^{2}-8\sqrt{2}\ x+15=0\ a\ pour\ racines\ \begin{cases}{\color{Red} x_{1}}=\frac{8\sqrt{2}-2\sqrt{17}}{2}={\color{Red} 4\sqrt{2}-\sqrt{17}} \\ {\color{Red} x_{2}}=\frac{8\sqrt{2}+\sqrt{17}}{2}={\color{Red} 4\sqrt{2}+\sqrt{17} }\end{cases}\\ \\ le\ couple{\color{Red} (x_{1} ; x_{2})}\ v\acute{e}rifier\ les\ deux\ \acute{e}galit\acute{e}s\ du\ syst\grave{e}me\ {\color{Magenta} \begin{cases}x^{2}+y^{2}=98\\xy=15 \end{cases}}\\ x^{2}+8\sqrt{2}\ x+15=0\ a\ pour\ racines\ \begin{cases}{\color{Red} x_{3}}=\frac{-8\sqrt{2}-2\sqrt{17}}{2}={\color{Red}- 4\sqrt{2}-\sqrt{17}} \\ {\color{Red} x_{4}}=\frac{-8\sqrt{2}+\sqrt{17}}{2}={\color{Red} -4\sqrt{2}+\sqrt{17} }\end{cases}\\$

$le\ couple{\color{Red} (x_{3} ; x_{4})}\ v\acute{e}rifier\ les\ deux\ \acute{e}galit\acute{e}s\ du\ syst\grave{e}me\ {\color{Magenta} \begin{cases}x^{2}+y^{2}=98\\xy=15 \end{cases}}$

$donc \ \ S=\left \{ {\color{Red} (4\sqrt{2}-\sqrt{17}}\ ;\ {\color{Red} 4\sqrt{2}+\sqrt{17} )}\ ;\ {\color{Red} (-4\sqrt{2}-\sqrt{17}}\ ;\ {\color{Red} -4\sqrt{2}+\sqrt{17} )} \right \}$

Exercice 6

vérifions que 10 x² - 3 x - 4 = 0 admet deux racines distincts dans

$10 x^{2} - 3 x - 4 = 0\ \ \ \Delta=(-3)^{2}-4\times 10\times (-4)=169> 0\\ \Delta> 0\ \ donc\ l'\acute{e}quation\ 10 x^{2} - 3 x - 4 = 0\ \\ admet\ deux\ racines\ {\color{Red} x_{1}}\ et\ {\color{Red} x_{2}}\ dans\ \mathbb{R}\\\\ calculons\ \ \frac{1}{{\color{Red} x_{1}}}+\frac{1}{{\color{Red} x_{2}}}\\ \frac{1}{{\color{Red} x_{1}}}+\frac{1}{{\color{Red} x_{2}}}=\frac{{\color{Red} x_{2}}+{\color{Red} x_{1}}}{{\color{Red} x_{1}x_{2}}} \\ or\ si \ a x^{2} +b x + c = 0\ admet\ deux\ racines\ dans\ \mathbb{R}\ alors \ on\ a\:\ \\ {\color{Red} S=x_{1}+x_{2}=\frac{-b}{a}}\ et\ {\color{Red} P=x_{1}x_{2}=\frac{c}{a}}\\ \\ Pour\ cet\ exercice\ on\ a\ {\color{DarkRed} S=\frac{3}{10}}\ et\ {\color{DarkRed} P=\frac{-4}{10}}\ \\donc\ {\color{DarkGreen} \frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{S}{P}=\frac{\frac{3}{10}}{\frac{-4}{10}}=\frac{-3}{4}}$

Exercice 7

$P(x)=x-2+ \frac{1}{x+1}\ \ \ ; (x\neq -1)$

montrons que P(x) = 0 admet deux racines distincts dans ℝ

$P(x)=x-2+ \frac{1}{x+1}=\frac{(x-2)(x+1)+1}{x+1}=\frac{x^{2}-x-1}{x+1}\\ \\ P(x)=0\Leftrightarrow \frac{x^{2}-x-1}{x+1} =0\Leftrightarrow x^{2}-x-1=0\ \ \ (x\neq -1)\\ \Delta=1+4=5> 0 \ \ ce \ qui\ montre\ que\\ P(x)\ admet\ deux\ racines\ {\color{Red} m}\ et\ {\color{Red} n}\ dans\ \mathbb{R}\\ \\ montrons\ que\ {\color{DarkRed} \frac{1}{m}+\frac{1}{n}=-1}\\ si \ a x^{2} +b x + c = 0\ admet\ deux\ racines\ dans\ \mathbb{R}\ alors \ on\ a\:\ \\ {\color{Red} S=x_{1}+x_{2}=\frac{-b}{a}}\ et\ {\color{Red} P=x_{1}x_{2}=\frac{c}{a}}\ \\ \\ on a : {\color{Blue} S=1}\ et\ {\color{Red} P=-1}\\ \\ {\color{DarkRed} \frac{1}{m}+\frac{1}{n}=\frac{n+m}{nm}=\frac{S}{P}=-1}$

الرياضيات

القائمة الرئيسية

الصفحات

Exercices Équations du second degré

أخر المواضيع من قسم : Lycée

Commentaires

Enregistrer un commentaire