Définition
Forme canonique du a x² + b x + c
Résolution de l 'équation a x² + b x + c = 0 ( a ≠ 0)
factorisation du trinômes a x² +b x +c ( a ≠ 0
Somme et produit des racines (Δ ≥ 0 )
Théorèmes
1) Équations du second degré ,factorisation
Définition :
toutes énoncé de forme a x² +b x + c = 0 ( a ≠ 0) est une équation du second degré à une seul inconnue x et a ; b ; et c sont des nombres réels . La valeur ou les valeurs que peut prendre x pour que l égalité soit vraie est l 'ensemble des racines ou solutions de l 'équation a x² + b x + c = 0 , on le note S
i) Forme canonique du a x² + b x + c
Montrons que ![\bg_white ax^{2}+bx + c =a\left [ \left ( x+\frac{b}{2a} \right )^{2}-\frac{b^{2}-4ac}{4a^{2}} \right ]](https://latex.codecogs.com/gif.latex?%5Cbg_white%20ax%5E%7B2%7D+bx%20+%20c%20%3Da%5Cleft%20%5B%20%5Cleft%20%28%20x+%5Cfrac%7Bb%7D%7B2a%7D%20%5Cright%20%29%5E%7B2%7D-%5Cfrac%7Bb%5E%7B2%7D-4ac%7D%7B4a%5E%7B2%7D%7D%20%5Cright%20%5D)
On pose Δ= b² - 4 a c s ' appelle le discriminant du trinômes a x² + b x + c( d équation a x² + bx +c = 0)
ii) Résolution de l 'équation a x² + b x + c = 0 ( a ≠ 0)
on a ![https://mathshas.blogspot.com/2020/01/equations-et-inequations-du-second-degre.html ax^{2}+bx+c=a\left [ \left (x+\frac{b}{2a} \right )^{2} -\frac{\Delta}{(2a)^{2}}\right ]](https://latex.codecogs.com/gif.latex?ax%5E%7B2%7D+bx+c%3Da%5Cleft%20%5B%20%5Cleft%20%28x+%5Cfrac%7Bb%7D%7B2a%7D%20%5Cright%20%29%5E%7B2%7D%20-%5Cfrac%7B%5CDelta%7D%7B%282a%29%5E%7B2%7D%7D%5Cright%20%5D) donc
donc
1er Cas :
2ème Cas:
3ème Cas:
A retenir:
Exercices 1
Résoudre dans ℝ:
iii) factorisation du trinômes a x² +b x +c ( a ≠ 0)
on a ![https://mathshas.blogspot.com/2020/01/equations-et-inequations-du-second-degre.html ax^{2}+bx+c=a\left [ \left (x+\frac{b}{2a} \right )^{2} -\frac{\Delta}{(2a)^{2}}\right ]](https://latex.codecogs.com/gif.latex?ax%5E%7B2%7D+bx+c%3Da%5Cleft%20%5B%20%5Cleft%20%28x+%5Cfrac%7Bb%7D%7B2a%7D%20%5Cright%20%29%5E%7B2%7D%20-%5Cfrac%7B%5CDelta%7D%7B%282a%29%5E%7B2%7D%7D%5Cright%20%5D)
Exercice 2
factoriser les polynômes suivants:
2) Somme et produit des racines (Δ ≥ 0 )
Théorème:
si Δ ≥ 0 Le trinôme admet admet deux racines 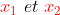 ou une seule racine donc
ou une seule racine donc  est la somme des racines et
est la somme des racines et 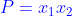 leur produit sont donnés par
leur produit sont donnés par  et
et 
Démonstration
Δ ≥ 0 donc


d' ici on peut écrire
Théorème:
Si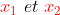 sont deux réels dont la somme est
sont deux réels dont la somme est  et le produit est
et le produit est 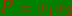 . Alors
. Alors 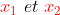 sont les deux solutions de l 'équation du second degré x² - S x + P = 0
sont les deux solutions de l 'équation du second degré x² - S x + P = 0
Exemple :
déterminer les nombres réels x et y tel que
S= x + y = 5 et P = x y = 4
cela revient à résoudre
à résoudre le système

donc on résout l équation x² - S x + P = 0 ⇔ x² - 5 x + 4 = 0
on a Δ= (- S ) ² - 4 P = 25 - 16 = 9
Δ > 0 donc l' équation admet deux solutions distincts
donc x = 1 et y = 4
1) calculer a et b
2) calculer a + b et a b ensuite
calculer
F(x)= - 4 x² +24 x - 28
Q(x) = -3 x² + x + 4
résoudre F(x)= 0 et Q(x) = 0

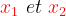
sans calculer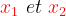 calculer
calculer 

montrer que P(x) = 0 admet deux racines distincts dans ℝ
si m et n deux solutions de P(x) = 0 montrer que
Démonstration
Δ ≥ 0 donc
d' ici on peut écrire
Théorème:
Si
Exemple :
déterminer les nombres réels x et y tel que
S= x + y = 5 et P = x y = 4
cela revient à résoudre
à résoudre le système
donc on résout l équation x² - S x + P = 0 ⇔ x² - 5 x + 4 = 0
on a Δ= (- S ) ² - 4 P = 25 - 16 = 9
Δ > 0 donc l' équation admet deux solutions distincts
donc x = 1 et y = 4
Exercice 3
soient a et b deux racines de l équation 4 x² - 7 x - 1 = 01) calculer a et b
2) calculer a + b et a b ensuite
calculer
exercice 4
1)ecrire la forme canonique des polynômes suivants :F(x)= - 4 x² +24 x - 28
Q(x) = -3 x² + x + 4
résoudre F(x)= 0 et Q(x) = 0
Exercice 5
Résoudre dans ℝ les systèmes suivants
exercice 6:
vérifier que l 'équation 10 x² - 3 x - 4 = 0 admet deux racines distinctssans calculer
Exercice 7
Soit le polynôme montrer que P(x) = 0 admet deux racines distincts dans ℝ
si m et n deux solutions de P(x) = 0 montrer que


Commentaires
Enregistrer un commentaire