1)Notion de logique(Introduction 1) variables 2) proposition 3) connecteurs logique 4)lois logiques)
2)Quantificateurs logiques

Introduction:

La logique mathématique est une science du raisonnement et du jugement (langages) qui ne tient pas compte du contenu. Elle a pour outils (ou éléments de base de la logique) des propositions et des variables.

1. Variables

Une variable est une grandeur dont la valeur peut même être inconnue, mais elle doit appartenir à un ensemble. Sur celle-ci est effectuée une combinaison d'opérations, soit avec des constantes, soit avec d'autres variables.

Exemples : 1) 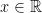$x\in \mathbb{R}$ x est une variable de 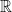$\mathbb{R}$ qui devient une constante quand elle prend une valeur donnée (x=4 ou x= a)

2) $f:E\rightarrow F\\x \rightarrow 2x+1$ x est appelée variable de f(x)

2) propositions

*) Une proposition(assertion) est un énoncé pouvant être vrai ou faux ( c'est à dire le sens qu'on peut attribuer à une expression ou à un énoncé)

On désigne généralement une proposition par une lettre : p; q; r....

Si la proposition p est vraie est noté par p ≡V ou 1

Si la proposition p est fausse est noté par: p ≡ F ou 0

Exemples :

. 1+4 =5 : vraie (V)

. 17=20 -3: vraie (V)

. 5+2 (n'est pas une proposition)

. $\left (\forall \ x\in\mathbb{R} \right )\ \ x+2> 3$ énoncé négociable pour la discussion tient :
Une proposition vraie sur l 'intervalle $]1 ;+\infty[$ $\left (x\in \ ]1 ;+\infty[ \right )$
Une proposition fausse sur l 'intervalle    $]-\infty ;1[$
**) Une proposition fonctionnelle est un énoncé mathématique qui a une signification et contient une variable (ou plusieurs variables) appartenant à un ensemble E et devient une proposition Chaque fois que nous remplaçons la variable avec une certaine valeur
Exemple:
déterminer les valeurs de la variable x pour lesquelles la proposition fonctionnelle suivante : $" (x\in\mathbb{Z}) :\left | x-3 \right |\leq 4 "$ est vraie
On a : $\left | x-3 \right |\leq 4\ \ donc \ -4\leq x-3\leq 4 \ alors \ -1\leq x\leq 7$ donc pour que la proposition soit vraie   x devrait prendre les valeurs suivantes:-1;0 ;1;2;3;4;5;6;7
***)  Proposition composé :est une proposition construite à partir de propositions simples reliées par des connecteurs logiques
exemple 1+0 =1 et 3+6 =9

pour décrire une proposition : on trace sa table de vérité : la proposition ne peut avoir que deux valeurs vraie (V)ou fausse(F) et non pas les deux

3) connecteurs logique

le connecteur est le mot qui marque un rapport de sens entre les propositions ou entre les énoncés.

les connecteurs servent essentiellement à construire, déduire de nouvelles propositions à partir des propositions de base et les propositions déjà formées

exemple:"il fait beau et 5 -4 =1" par la conjonction et on obtient la proposition composée
a)négation d'une proposition
Une proposition prenant la valeur de vérité opposée à celle de p est la négation de p . On la note non p ou ¬p
exemple: p: $''1> \sqrt{2}''$ sa négation est : non p : $''1\leq \sqrt{2}''$

les valeurs de vérité de P et $\neg$ P et $\bg_white \neg\left ( \neg\ p \right )$ sont représentées dans la table de vérité ci- contrela négation de la négation d'une proposition est la proposition elle même
b)Conjonction de deux propositions:
si on relie deux proposition par le mot "et" on obtient une proposition composée dite la conjonction de deux proposition on la note "p et q" ou $p\ \wedge\ q$
les valeurs de vérité de $p\ \wedge\ q$ sont représentées dans la table de vérité ci- contre $p\ \wedge\ q$ est vraie lorsque les deux propositions sont vraies ,autrement la conjonction est fausse si l'une des deux propositions est fausse

exemples : 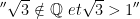$''\sqrt{3}\notin \mathbb{Q}\ et \sqrt{3}> 1''$ est une proposition vraie

$''\pi \in \mathbb{Q}\ \ et\ \sqrt{2}> 1''$ est une proposition fausse

Remarque : le symbole 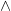$\wedge$ rappelle celui de l 'intersection 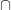$\cap$ qui désigne : si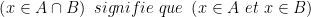 $\left (x\in A\cap B \right )\ signifie\ que\ \left (x\in A\ et\ x\in B \right )$

c)Disjonction de deux propositions:

si on relie deux proposition par le mot "ou" on obtient une proposition composée dite la disjonction de deux proposition on la note "p ou q" ou 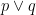$p\vee q$

les valeurs de vérité de 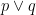$p\vee q$ sont représentées dans la table de vérité ci- contre 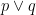$p\vee q$ est vraie si l'une des propositions est vraie autrement dit 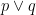$p\vee q$ est fausse si les deux propositions sont fausse

exemples:

$''\sqrt{3}\notin \mathbb{Q}\ ou\ 2= 5''$ est une proposition vraie

$''\forall x\in \mathbb{R}:x^{2}< 0 \ ou\ 4-1 =5''$ est une proposition fausse

remarques:

*) Le « ou » en français n'est pas le « ou » de la logique Il est parfois inclusif et parfois exclusif

le « ou » est inclusif ( l'addition des deux possibilités à la fois) .

Mais dans le langage courant le« ou » prend une valeur exclusive (ambigu)( l'addition des deux possibilité est exclue).

exemple:

On recherche un professeur qui connaisse le mathématique ou la physique . dans cette phrase il suffit que le professeur recherché connaitre une seule de ces deux matière ou les deux à la fois.(ici « ou » est inclusif )

dans d'un restaurant on lit "Le menu du jour propose du dessert ou de formage" dans cette phrase le « ou » est exclusive . Pour éviter toutes ambiguïté on devrait dire :"Le menu du jour propose du dessert ou bien de formage" ( autrement : "Le menu du jour propose soit du dessert soit de formage")

**) le symbole 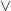$\vee$ rappelle celui de la réunion 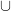$\cup$ qui désigne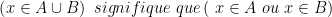 $\left (x\in A\cup B \right )\ signifique\ que \left (\ x\in A\ ou\ x\in B \right )$

d) implication (proposition conditionnelle)

la proposition p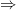 $\Rightarrow$ q se lit "p implique q" ou" si p alors q" est fausse lorsque l'on a simultanément la proposition p vraie et la proposition q fausse , la proposition p 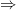$\Rightarrow$ q est vraie dans tous les autres cas

dans p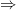 $\Rightarrow$ q , p est l'antécédent de l'implication et q le conséquent de l'implication , qui indique une relation logique où le conséquent découle logiquement de l'antécédent

On peut exprimer "p implique q" par :p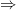 $\Rightarrow$ q = $\neg\ p \vee q$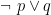

les valeurs de vérité de p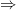 $\Rightarrow$ q sont représentées dans la table de vérité ci- contreExemples:

e)transitivité de l’implication:

soient p , q et r des propositions mathématiques: si p implique q et q implique r alors p implique r c'est à dire 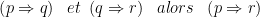$\left (p\Rightarrow q \right )\ \ et \ \left (q\Rightarrow r \right )\ \ alors\ \ \left (p\Rightarrow r \right )$
f)l'équivalence logique(proposition biconditionnelle )
La proposition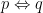 $p\Leftrightarrow q$ ou ( p si et seulement si q) ou (p équivalent à q) est vraie lorsque l 'on a simultanément p et q vraies ou fausses .la proposition est fausse dans les autres cas
les valeurs de vérité de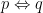 $p\Leftrightarrow q$ sont représentées dans la table de vérité ci-dessous
exemples:
Remarque :lorsque p est équivalent à q
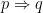$p\Rightarrow q$ donc p est une condition suffisante de q ( q est une condition nécessaire de p)
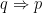$\bg_white q\Rightarrow p$ donc q est une condition suffisante de p ( p est une condition nécessaire de q)
p est une condition nécessaire et suffisante de q et inversement
donc pour démontrer une équivalence logique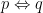 $p\Leftrightarrow q$ la démonstration se fait en deux étapes :
i) démontrer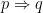 $\bg_white p\Rightarrow q$
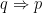
ii) démontrer $\bg_white q\Rightarrow p$

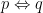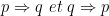Le tableau ci-dessous montre que $\bg_white p\Leftrightarrow q$ et $p\Rightarrow q\ et\ q\Rightarrow p$ ont même table de vérité

4)lois logiques
loi logique est une proposition composée qui est vraie quelles que soient les valeurs de vérité des propositions qui la compose

Exemple: "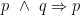 $p\ \wedge\ q\Rightarrow p$ "pour vérifier que cette proposition est une loi logique on construit sa table de véritéOn remarque que la dernière colonne est formée uniquement de la valeur V

d'autres propositions composées dites lois logiques sont les suivantes: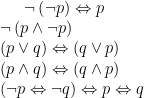 $\neg\left ( \neg p \right )\Leftrightarrow p\\ \neg\left ( p\land\neg p \right )\\ \left (p\vee q \right )\Leftrightarrow \left (q\vee p \right )\\ \left (p\land q \right )\Leftrightarrow\left ( q\land p \right )\\ \left (\neg p\Leftrightarrow \neg q \right )\Leftrightarrow p\Leftrightarrow q$

الرياضيات

القائمة الرئيسية

الصفحات

Notion de logique

3)Propriétés des quantificateurs

4)réciproque et contraposée

5Différents types de démonstrations

Introduction:

La logique mathématique est une science du raisonnement et du jugement (langages) qui ne tient pas compte du contenu. Elle a pour outils (ou éléments de base de la logique) des propositions et des variables.

1. Variables

Une variable est une grandeur dont la valeur peut même être inconnue, mais elle doit appartenir à un ensemble. Sur celle-ci est effectuée une combinaison d'opérations, soit avec des constantes, soit avec d'autres variables.

Exemple: " $p\ \wedge\ q\Rightarrow p$ "pour vérifier que cette proposition est une loi logique on construit sa table de véritéOn remarque que la dernière colonne est formée uniquement de la valeur V

أخر المواضيع من قسم : Lycée

Commentaires

Enregistrer un commentaire

القائمة الرئيسية

الصفحات

Notion de logique

3)Propriétés des quantificateurs

4)réciproque et contraposée

5Différents types de démonstrations

Introduction:

La logique mathématique est une science du raisonnement et du jugement (langages) qui ne tient pas compte du contenu. Elle a pour outils (ou éléments de base de la logique) des propositions et des variables.

1. Variables

Une variable est une grandeur dont la valeur peut même être inconnue, mais elle doit appartenir à un ensemble. Sur celle-ci est effectuée une combinaison d'opérations, soit avec des constantes, soit avec d'autres variables.

Exemple: " "pour vérifier que cette proposition est une loi logique on construit sa table de véritéOn remarque que la dernière colonne est formée uniquement de la valeur V

أخر المواضيع من قسم : Lycée

Commentaires

Enregistrer un commentaire

Exemple: " $p\ \wedge\ q\Rightarrow p$ "pour vérifier que cette proposition est une loi logique on construit sa table de véritéOn remarque que la dernière colonne est formée uniquement de la valeur V