Équations , inéquations du premier degré et systemes

Rappels
Équations du premier degré  à une inconnue
Inéquations du premier degré  à une inconnue
Équation du premier degré a deux inconnues
Systèmes d'équations du premier degré à deux inconnues
1)Rappels

Résoudre dans ℝ les équations suivantes:

 d'où S={0}

2)Équations du premier degré  à une inconnue

Définition:

Toutes expression de la forme a x +b =0 est une équation du premier degré à une inconnue x ( ou équation affine )  où a et b sont deux nombres réels . Les valeur de l'inconnue x qui rend l'égalité  vraie est les  solutions de l'équation a x  + b =0 , l'ensemble des solutions qui vérifier cette égalité est l'ensemble de solution de l'équation  on le note souvent par S

i)Résolution de l 'équation a x +b =0 dans ℝ

Si a ≠ 0  l'équation a x +b = 0 admet comme solution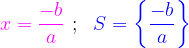  

Si  a = 0 et b = 0  l'équation  0 x = 0  admet comme solution l 'ensemble des nombres réels , S = ℝ 
Si a = 0 et b ≠ 0 l'équation 0 x + b = 0 ⇔ 0 x = - b n'admet pas

de solution S = { } ou S=∅
Exemples :
3 x + 1 =0  ⇔ 3 x = - 1 donc la solution est   x = - 1/3 , S = {-1/3}
2 x - 3( x + 1) = - x - 3⇔ - x - 3 = - x  - 3 ⇔  0 x = 0 donc la solution 
est l 'ensemble ℝ , S = ℝ
3 x +1 = - 3( √2 - x ) ⇔ 3 x - 3 x  = - 3√2 - 1  ⇔ 0 x = - 3√2 - 1  n'admet pas 
de solution S=∅
ii) Résolution de l 'équation de type ( a x +b )( c x +d ) = 0
On a ( a x +b)( c x +d ) = 0 signifie que a x +b = 0 ou c x +d = 0
Donc pour résoudre  une équation de type ( a x +b )( c x +d ) = 0 revient  à résoudre deux équations de type a x  + b =0
( a x +b )( c x +d ) = 0 ⇔ a x +b =0 ou  c x +d =0 
Exemples: 
résoudre dans ℝ
1) x² - 2 x = 0      ;     2) ( x - 1) ( x + 2)( - 3√2 x + 1) = 0
solutions:
1) x² - 2 x = 0 ⇔  x ( x - 2 ) = 0 ⇔  x = 0 ou x = 2 donc S= { 0 ; 2}
2)  ( x - 1) ( x + 2)( - 3√2 x + 1) = 0 ⇔ x - 1 =0 ou x + 2 = 0 ou  - 3√2 x + 1 = 0 donc 
les solutions sont : x = 1 ou x = - 2 ou  x = 1/3√2 = √2/6  et  S ={ - 2; √2/6 ; 1 }
3)Inéquations du premier degré  à une inconnue

i) Résolution de l 'inéquation du premier degré

Définition : 
Toutes écriture de la forme a x +b ≤ 0 ou  a x +b ≥ 0 ou a x +b < 0 ou a x +b > 0 (où a et b sont deux nombres réels, a ≠ 0 ) est une  inéquation du premier degré à une inconnue x , l 'ensemble des valeurs que peut prendre x  pour que l 'inégalité soit vraie est appelé ensemble de solution  de l 'inéquation on le note  S

A résoudre dans ℝ   a x +b < 0

Si a ≠  et a > 0 
a x +b < 0 ⇔ a x < - b ⇔  x <  - b /a  donc l'ensemble de solution est :
S= ] - ∞ ; - b /a [

Si a ≠  et a < 0 

a x +b < 0 ⇔ a x < - b ⇔  x >  - b /a  donc l'ensemble de solution est :
S= ]- b /a ; + ∞ [

Si a = 0 et b > 0 ( - b < 0 )

a x +b < 0 ⇔ a x < - b dans ce cas on a une contradiction car un nombre négatif est toujours inférieur à zéro et par suite S=∅

 Si  a = 0 et b < 0 ( - b > 0 )

a x +b < 0 ⇔ a x < - b ⇔ 0 x < - b  dans ce cas la solution est l 'ensemble ℝ ( car 0 est  toujours inférieur à tous nombre positif  et par suite S= ℝ

En résumant tous par le diagramme suivant

Exemples:

Signe de a x +b ; a ≠ 0

Résolvons l'équation a x +b = 0 

 a x +b = 0 ⇔ x = - b/a

Propriété:

a x +b est du signe de a pour les valeurs de x supérieures à la valeur 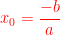 qui annule a x +b

Exercices d'application

1) Résoudre dans ℝ les équations suivantes:

2) trouver le signe des fonctions affines suivantes:

 en déduire les solutions  des inéquations suivantes: 

3) Résoudre dans ℝ  l'inéquation suivante:

voir solution ici

4) Équation du premier degré a deux inconnues

1) Définition: 

toutes écriture de la forme  a x + b y + c = 0 est une équation du premier degré  a deux inconnues  x et y  ;  a , b et c sont des nombres réels (  a ≠ 0  et b ≠ 0 )

les valeurs  du couple (x ; y)  qui rend l 'égalité vraie  c'est l'ensemble de solution de l'équation a x + b y + c = 0

2) solution de l équation a x + b y + c =0

 Pour résoudre  l 'équation  du type  a x + b y + c = 0 , on utilise  l' une des méthodes suivantes : 

Soit on calcul x en fonction de y 

soit  on calcul y en fonction de x 

Exemple: 

Résoudre dans ℝ ² l'équation  : 2 x - y +3 = 0

méthode 1  : y en fonction de x

2 x - y + 3 = 0  ⇔ - y =  - 3 - 2 x ⇔  y = 2 x + 3

donc  l 'ensemble de solution est  :

S = {  ( x ; y ) ∈ ℝ ² /  y = 2 x + 3 }  ou S = { ( x ; 2 x + 3 ) / x ∈ ℝ }

méthode 2  : x  en fonction de y 

2 x - y + 3 = 0 ⇔   x = -3 + y / 2 = y  - 3 / 2

S = {  ( x ; y ) ∈ ℝ ² /  x = y  - 3 / 2 }  ou S = { ( y  - 3 / 2 ; y ) / y ∈ ℝ }

5)Systèmes d'équations du premier degré à deux inconnues