Polynômes

Définition :

Egalité de deux polynômes :

Somme de deux polynômes :

Produit de deux polynômes :

Division euclidienne 

Racine d'un polynôme :

Factorisation d'un polynôme

1) Polynômes :

1) Polynômes :

i) Définition :

Un polynôme est une expression littérale de la forme :

 $P(x)= a_{n}x^{n}+a_{n-1}x^{n-1}+......+a_{2}x^{2}+a_{1}x+a_{0}$ avec $a_{n};a_{n-1}; ......; a_{2};a_{1};a_{0}$ ($a_n\neq 0$) sont les coefficients du polynôme et $a_{0}$ est le terme constant

Le degré du polynôme $P$ est $n$ on le note $d°P= deg P= n$

 

Exemples :

$P(x)=a x+b$ est un polynôme de degré $1$ : $d°P= 1$

$G(x)= a x²+b x +c$ est un polynôme de degré $2$   $d°G= 2$

$E(x)= 0$ est un polynôme nul, le polynôme $E$ n 'a pas de degré

$F(x) = c$   est un polynôme constant ($c$ ∈ ℕ*) $d°F= 0$

 

ii)Egalité de deux polynômes :

Deux polynômes sont égaux s ils ont même degré et les coefficients des termes (les coefficients des monômes) qui ont même exposant sont égaux

 

Exemples :

$P(x)=2 x² +3 x +6$   et $Q(x) = 2 x² +3 x +6 et F(x) = 2 x² +3 x$

$P(x) = Q(x) mais P(x) ≠ F(x)$

 

Exercice d'application :

Soient deux polynômes suivants :

$G(x)= 3x^{4}+2x^{3}-7x^{2}+3$

 $H(x)=3x^{4}+(2a+1)x^{3}+(b-3)x^{2}+(2c+3)x+ d$

Déterminons $a, b , c \ et\  d$ sachant que $G(x) = H(x)$ 

Puisque $G(x) = H(x)$ alors

$\left\{ \begin{matrix}2a+1=2\\ b-3=-7\\ 2c+3=0\\ d=3 \end{matrix} \right\} \Leftrightarrow \left\{ \begin{matrix}2a=1\\ b=-4\\ 2c=-3\\ d=3 \end{matrix} \right\}$  donc $\left\{ \begin{matrix}a=1/2 \\ b=-4\\ c =-3/2\\ d=3 \end{matrix} \right\}$

 

iii)Somme de deux polynômes :

 

Soient $P(x)=5x^{2}+4x-3$ et

$Q(x)=-3\sqrt{5}x^{3}+2x^{2}-2x+2$

Calculons $F(x) + Q(x) \ et\  F(x) - Q(x)$

$P(x)+Q(x)= 5x^{2}+4x-3+(-3\sqrt{5}x^{3}+2x^{2}-2x+2)$

$=-3\sqrt{5}x^{3}+(5+2)x^{2}+(4-2)x-3+2$

$=-3\sqrt{5}x^{3}+7x^{2}+2x-1=(P+Q)(x)$

$d°(P+Q)=3= d°Q$

$P(x)-Q(x)= 5x^{2}+4x-3-(-3\sqrt{5}x^{3}+2x^{2}-2x+2)$

 $=3\sqrt{5}x^{3}+(5-2)x^{2}+(4+2)x-3-2$ $=3\sqrt{5}x^{3}+3x^{2}+6x-5=(P-Q)(x)$

$d°(P - Q)=3= d°Q$

Propriété : 

La somme de deux polynômes P et Q est aussi un polynôme noté $P + Q$  

$d°( P + Q) ≤ sup ( d°P ; d°Q )$

 

iiii) Produit de deux polynômes :

 

Soient :$P(x)=5x^{2}+4x-3$

$Q(x)=5x^{3}+2x^{2}-2x+2$

Calculons $P(x) × Q(x)=(P×Q)(x)$

$P(x)\times Q(x)=(5x^{2}+4x-3)\times( 5x^{3}+2x^{2}-2x+2$

 $=5x^{2}(5x^{3}+2x^{2}-2x+2)+4x(5x^{3}+2x^{2}-2x+2)-3(5x^{3}+2x^{2}-2x+2)$

 $=25x^{5}+10x^{4}-10x^{3}+10x^{2}+20x^{4}+8x^{3}-8x^{2}+8x-15x^{3}-6x^{2}+6x-6$

$=25x^{5}+30x^{4}-17x^{3}-4x^{2}+14x-6$

$=(P\times Q)(x)$

$d°(P ×Q)=5=d°P +d°Q=2+3$

 

Propriété :

Le produit de deux polynômes $P$ et $Q$ est un polynôme noté $P × Q$

  $d°(P ×Q)=d°P +d°Q$

Remarque :

Si $\alpha \in \mathbb{R^{*}}$ et $P$ un polynôme alors $\alpha P$ est aussi un polynôme de meme degré que $P$

 

2)Division euclidienne

اقرا ايضاcalcul trigonométrique

اقرا ايضاsuites numériques

اقرا ايضاgénéralités sur les fonctions

اقرا ايضاParité dune fonction

i)Racine d'un polynôme :

Soit le polynôme :$P(x)=x ^ {4} +x^ {3} +x^ {2} -x-2$

Vérifiant que $P (1) =0$   et  $P (-1) =0$

$P (-1) = (-1) ^ {4} +(-1) ^ {3} +(-1) ^ {2} -(-1) -2$

$=1-1+1+1-2=0$

$P (1) = (1) ^ {4} +(1) ^ {3} +(1) ^ {2}-(1) -2$

$=1+1+1-1-2=3-3=0$

On dit que $(-1)$ et $1$ sont les racines de $P(x)$ ou zéro de $P(x)$

Définition : la racine d'un polynôme $P$ c'est la valeur a qui annule le polynôme

$a$ est une racine de $P(x)$ est équivalent à $P(a)=0$

 

ii)Division euclidienne

Pour l 'Exemple $P(x)=x ^ {4} +x^ {3} +x^ {2} -x-2$

$P (2) =2 ^ {4} +2^ {3} +2^ {2} -2-2$

        $=16+8+4-2-2=24\neq 0$

Puisque $P (2) ≠0$ donc $2$ n 'est pas une racine de $P(x)$

$P(x)-P(2)$

$=x^{4}+x^{3}+x^{2}-x-2 -(2^{4}+2^{3}+2^{2}-2-2 )$

$=(x^{4}-2^{4})+(x^{3}-2^{3})+(x^{2}-2^{2})-(x-2)-2+2$

$= (x^{4}-2^{4})+(x^{3}-2^{3})+(x^{2}-2^{2})-(x-2)$

 $=(x^{2}-2^{2})(x^{2}+2^{2})+(x-2)(x^{2}+2x+2^{2})+(x-2)(x+2)-(x-2)$

$=(x-2)\left ((x+2)(x^{2}+2^{2})+(x^{2}+2x+2^{2})+(x+2)-1 \right )$

$=(x-2)\left ( x^{3}+4x+2x^{2}+8+x^{2}+2x+4+x+2-1 \right )$

 $=(x-2)(x^{3}+3x^{2}+7x+13)$

$P(x)-P(2)=(x-2)(x^{3}+3x^{2}+7x+13)\\ d' o\grave{u}\ P(x)=(x-2)(x^{3}+3x^{2}+7x+13)-P(2)$

$P(x)=(x-2)Q(x)-P(2)$ 

avec $Q(x)= (x^{3}+3x^{2}+7x+13)$ et $d°Q=d°P - 1=4 - 1=3$ et $d°Q=d°P - 1=4 - 1=3$

 

Propriété :

Soit P(x) un polynôme de degré $n$ ( $n$∈ℕ*) et $a$ ∈ℝ , il existe un polynôme $Q(x)$  tel que 

$P(x)= (x-a) Q(x) +P(a)$

$Q(x)$ est le quotient de la division euclidienne de $P$ sur $(x - a)$

Exemple :

$P(x)=x^ {3} +x^ {2} -5x-21$ est divisible par $(x-3)$ car $3$ est une racine de $(P(x) (P (3) =0)$

 

Définition :

Soit $P(x)$ un polynôme de degré $n$ , $P(x)$ est divisible par $(x -a)$ ( $a$ racine de $P(x) )$ s’il existe un polynôme $Q(x)$ de degré $(n-1)$ tel que $P(x)= (x-a)Q(x)$

 

Exercice d'application :

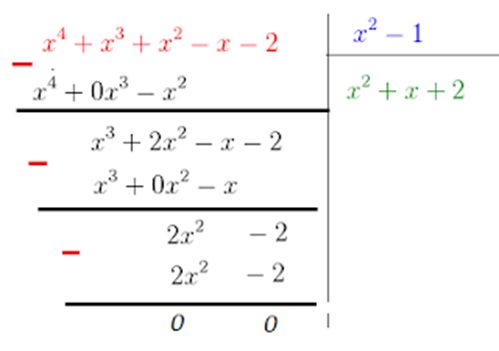
Soit le polynôme : $P(x)=x ^ {4} +x^ {3} +x^ {2} -x-2$

 En utilisant la division euclidienne

Déterminer les réels b et c tels que $P(x) = (x²-1) (x² +b x +c)$

Pour trouver $b$ et $c$ effectuant la division de $P(x)$ par $(x² - 1)$

D’où     $P(x)$=$(x^{2}-1)$ $(x^{2}+x+2 )$ et par suite $b=1 \ et\  c=2$

 

 

Propriété

$P(x)$ un polynôme degré de $P$ supérieur ou égale à $1$($d°P ≥ 1$), le polynôme est divisible par $x-a$  si  $a$ est racine de polynôme $P(x)$

 

iii)factorisation d'un polynôme

 

Propriété :

si $a$ est une racine de polynôme $P(x)$, alors le polynôme $P(x)$ peut être mis sous forme d 'un produit de facteurs dont l'un est $(x-a)$

En général si  $a_{1};a_{2};a_{3};.....;a_{n}$ sont les racines de polynôme $P(x)$ alors $P(x)$ peut se mettre sous la forme $P(x)= (x-{\color{Red} a_{1}})(x-{\color{Red} a_{2}})(x-{\color{Red} a_{3}}).....(x-{\color{Red} a_{n}})Q(x)$  où. $Q(x)$ est un polynôme tel que

 $d°P=(d°Q)+n$ ($n$ : nombre de racine de $P(x)$ )

Exemple :

$P(x)= 2x^{4}-3x^{3}-12x^{2}+7x+6$

Vérifiant que $1 ; -2 ; 3 \ et\  \frac{-1}{2}$ sont les racines de $P(x)$

On a$P(1)= 2\times 1^{4}-3\times 1^{3}-12\times 1^{2}+7\times 1+6$

 

 

$=2+7+6-3-12=15-15=0$

 

$P(1)=0$

 

$P(-2)$

$= 2\times (-2)^{4}-3\times (-2)^{3}-12\times (-2)^{2}+7\times (-2)+6$

 

 $=32+24-48-14+6\\ =56+6-48-14=62-62=0$

 

$P(3)= 2\times (3)^{4}-3\times (3)^{3}-12\times (3)^{2}+7\times (3)+6$

 

 $=162-81-108+21+6$ $=189-189=0$ 

 

 $P(3)=0$  

 $P(\frac{-1}{2})= 2\times \left (\frac{-1}{2} \right )^{4}-3\times \left (\frac{-1}{2} \right )^{3}-12\times \left (\frac{-1}{2} \right )^{2}+7\times \left ( \frac{-1}{2} \right )+6$

 

 $=\frac{2}{16}+\frac{3}{8}-\frac{12}{4}-\frac{7}{2}+6$

 

$=\frac{1+3-24-28+48}{8}$

 

 $=\frac{52-52}{8}=0$ $P(\frac{-1}{2})=0$

 

le polynôme $P(x)= 2x^{4}-3x^{3}-12x^{2}+7x+6a$ quatre racines $1 ; -2 ; 3 \ et\  -1/2$ ,donc on peut mettre $P(x)$ sous forme :

 

$P(x)= (x-1)(x+2)(x-3)(x+1/2)Q(x)$ 

 

avec $d°Q=d°P-4=4-4=0$ et 

 $Q(x)=\frac{P(x)}{(x-1)(x+2)(x-+3)(x+\frac{1}{2})}$

 

$=\frac{2x^{4}-3x^{3}-12x^{2}+7x+6}{x^{4}-\frac{3x^{3}}{2}-\frac{12x^{2}}{2}+\frac{7x}{2}+3}$

 

$= 2\left (\frac{2x^{4}-3x^{3}-12x^{2}+7x+6}{2x^{4}-3x^{3}-12x^{2}+7x+6} \right )=2 Q(x)=2$

 

 

 

Exercice d'application :

Soit $P(x)=4x^4-20x^3+29x^2-16x+3$

1)vérifier que $P(1) =0$

2)Trouver le polynôme $Q(x)$ tel que $P(x)=(x-1)Q(x)$

3) déterminer les racines de Q(x) en déduire les racines de $P(x)$

4) factoriser $P(x)$

Solution ICI