Résolution d'équation et l 'inéquation

ÉNONCÉ ICI
1) Résoudre dans ℝ les équations suivantes:

$1)\ \frac{6x+1}{3}-x=\frac{2x-1}{2}$

$\frac{6x+1}{3}-x=\frac{2x-1}{2}\Leftrightarrow \frac{6x+1-3x}{3}=\frac{2x-1}{2}\\ \\ \Leftrightarrow 2(3x+1)=3(2x-1)\Leftrightarrow 6x+2=6x-3\Leftrightarrow 0x=-5$ donc l'équation n'admet pas

de solution d' ou S=∅

$2)\ x^{2}-1+4(x^{2}-1)=0$

$\ x^{2}-1+4(x^{2}-1)=0\Leftrightarrow (x^{2}-1)(1+4)=0\\ \Leftrightarrow5(x-1) (x+1)=0\Rightarrow x-1=0\ \ ou\ \ x+1=0\ \ \\ d'o\grave{u}\ \ {\color{Red} x=1}\ ou\ {\color{Red} x=-1}$ S={- 1 ; 1}

$3)\ (4x-3)(1-2x)-(4x-3)^{2}=0$

$\ (4x-3)(1-2x)-(4x-3)^{2}=0\Leftrightarrow (4x-3)\left ((1-2x)-(4x-3) \right )= 0 \\ \Leftrightarrow (4x-3)(4-6x)=0\Rightarrow 4x-3=0\ ou\ 4-6x=0\\ d'o\grave{u}\ {\color{Red} x=\frac{3}{4}}\ ou\ {\color{Red} x=\frac{2}{3}}\ \ donc\ \ {\color{Blue} S=\left \{ \frac{2}{3};\frac{3}{4} \right \}}$

2) trouver le signe des fonctions affines suivantes:

$1)-2x+1$

- 2 x +1 = 0 ⇔ - 2 x = - 1 ⇔ x = 1/2

tableau de signe de - 2 x +1 en fonction de x

d'Après tableau de signe de - 2 x +1

en déduit que - 2 x +1 < 0 si ${\color{Red} x\in \ ]\frac{1}{2}\ ;+\infty[}$ donc ${\color{Blue}S=\ ]\frac{1}{2}\ ;+\infty[}$

$2)\sqrt{2}-\sqrt{3}\ x$

$\sqrt{2}-\sqrt{3}\ x=0\Leftrightarrow -\sqrt{3}\ x=-\sqrt{2}\Leftrightarrow {\color{Red} x=\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}}$

tableau de signe de ${\color{Red} \sqrt{2}-\sqrt{3}\ x}$ en fonction de x

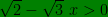d'Après tableau de signe de ${\color{Red} \sqrt{2}-\sqrt{3}\ x}$ en déduit que $\bg_green \sqrt{2}-\sqrt{3}\ x> 0$ si ${\color{Red}x\in\ ]-\infty;\frac{\sqrt{6}}{3}[}$ donc ${\color{Blue}S= ]-\infty;\frac{\sqrt{6}}{3}[}$

3) Résoudre dans ℝ l'inéquation suivante:

$\bg_green 1)\ 4x^{2}-25\geq 0$

$\bg_white 4x^{2}-25\geq 0\ signifie\ que\ (2x-5)(2x+5)\geq 0$

$(2x-5)(2x+5)\geq 0$ ⇔ 2 x +5 ≤ 0 et 2 x - 5 ≤ 0 ou 2 x +5 ≥ 0 et 2 x - 5 ≥ 0

⇔ x ≤ - 5/2 et x ≤ 5/2 ou x ≥ - 5/2 et x ≥ 5/2

⇔ x ∈ (] - ∞ ; -5/2 [ ∩ ] - ∞ ; 5/2 [ ) ou x ∈ ( [ -5/2 ; +∞ [ ∩ [ 5/2 ; +∞ [ )

⇔ x ∈] - ∞ ; -5/2 [ ou x ∈ [ 5/2 ; +∞ [

⇔ x ∈ ( ] - ∞ ; -5/2 ] ∪ [ 5/2 ; +∞ [ )

d' une autre méthode :

Résoudre 4 x² - 25 = 0 ⇔ 2 x + 5 = 0 ou 2 x - 5 = 0 ⇔ x = - 5/2 ou x = 5/2
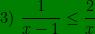
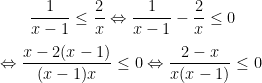
d'où tableau de signe de 4 x² - 25 en fonction de x

ce qui montre que 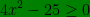$\bg_green \ 4x^{2}-25\geq 0$ si x ∈ ( ] - ∞ ; -5/2 ] ∪ [ 5/2 ; +∞ [ )

donc S=] - ∞ ; -5/2 ] ∪ [ 5/2 ; +∞ [

$2)\ \frac{3x-1}{\sqrt{3}-3}< \frac{3x-2}{\sqrt{3}+3}$

$\frac{3x-1}{\sqrt{3}-3}< \frac{3x-2}{\sqrt{3}+3}\Leftrightarrow \frac{(\sqrt{3}+3)(3x-1)}{3-9}< \frac{(\sqrt{3}-3)(3x-2)}{3-9}\\ \\ \\ \Leftrightarrow -(\sqrt{3}+3)(3x-1)< -(\sqrt{3}-3)(3x-2)\\ \Leftrightarrow 3\sqrt{3}\ x-\sqrt{3}+9x-3> 3\sqrt{3}\ x-2\sqrt{3}-9x+6\\ \Leftrightarrow 18x-9+\sqrt{3}> 0\Leftrightarrow x> \frac{9-\sqrt{3}}{18}\simeq 0,4037$

donc ${\color{Blue} x\in ]\frac{9-\sqrt{3}}{18} ;+\infty[}\ \ et\ {\color{Red} S= ]\frac{9-\sqrt{3}}{18} ;+\infty[}$

$3)\ \frac{1}{x-1}\leq \frac{2}{x}$

$\ \frac{1}{x-1}\leq \frac{2}{x}\Leftrightarrow \frac{1}{x-1}- \frac{2}{x}\leq 0\\ \\ \Leftrightarrow \frac{x-2(x-1)}{(x-1)x}\leq 0\Leftrightarrow \frac{2-x}{x(x-1)}\leq 0$

tableau de signe de 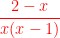${\color{Red} \frac{2-x}{x(x-1)}}$ en fonction de x ( avec x ≠ 0 et x ≠ 1 )

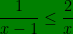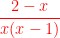les solutions de l inéquation $\bg_green \frac{1}{x-1}\leq \frac{2}{x}$ ce déduit à partir du tableau de signe ${\color{Red} \frac{2-x}{x(x-1)}}$ en fonction de x donc S = ] 0 ; 1 [ ∪ [ 2 ; +∞ [

$4)\ \frac{x-1}{x}-\frac{1}{x+1}\leq \frac{2x-1}{x(x+1)}$
$\bg_white \frac{x-1}{x}-\frac{1}{x+1}\leq \frac{2x-1}{x(x+1)}\Leftrightarrow \frac{(x-1)(x+1)-x}{x(x+1)}\leq \frac{2x-1}{x(x+1)}\ \ {\color{Magenta} (avec\ x\neq 0\ et\ x\neq -1)}\\ \\ \\ \Leftrightarrow (x-1)(x+1)-x\leq 2x-1\\ \\ \Leftrightarrow (x-1)(x+1)-x+1\leq 2x\\ \\ \Leftrightarrow (x-1)(x+1)-(x-1)-2x\leq 0\\ \\ \Leftrightarrow (x-1)\left ((x+1)-1 \right )-2x\leq 0\\ \\ \Leftrightarrow x(x-1)-2x\leq 0\\ \\ x\left ( (x-1)-2 \right )\leq 0\\ \\ \Leftrightarrow x(x-3)\leq 0$
$x(x-3)\leq 0\ signifie\ que\ x\leq 0\ et\ (x-3)\geq 0\ \ ou \ x\geq 0\ \ et\ \ (x-3)\leq 0\\ \\ \acute{e}quivalent\ \grave{a}\ x\in\left [ \left (]-\infty ; 0[\cap ]3; +\infty[ \right )\ \cup\ \left ( ]0 ; +\infty[ \ \cap ]-\infty ; 3] \right ) \right ]\\ \Leftrightarrow x\in ]0 ; 3]$
l' ensemble de solution de l 'inéquation
$4)\ \frac{x-1}{x}-\frac{1}{x+1}\leq \frac{2x-1}{x(x+1)}$ est S = ]0 ; 3]

même résultats si on trace tableau de signe de x ( x - 3 ) en fonction de x

x ( x - 3 ) ≤ 0 sur l' intervalle ]0 ; 3]

الرياضيات

القائمة الرئيسية

الصفحات

Résolution d'équation et l 'inéquation

أخر المواضيع من قسم : Lycée

Commentaires

Enregistrer un commentaire