القائمة الرئيسية

الصفحات

تعديل المشاركة

Systèmes d'équations du premier degré à deux inconnues

has
(0)

Équations , inéquations du premier degré et systemes

             1)Définition
        2)Méthodes de résolution
1)Définition :
Un systèmes d’équations du premier degré à deux inconnues est constitué de deux égalité, chaque égalité contient deux inconnues, notées x et  y
Résoudre  un système\bg_white \small \bg_blue\ {\color{Red}( S)}\ \begin{cases}ax+by+c=0\\ a'x+b'y+c'=0\end{cases}c'est trouver le coupe (x ; y) qui rend les deux égalités vraies
Exemple :{\color{Red} \begin{cases}2x-y+1=0\ {\color{Blue} \ \ (1)}\\ 4x+y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
2)Méthodes de résolution 
Pour résoudre un système d’équation, On utilise l 'une des méthodes suivantes
i)Méthode de substitution : 
c'est on calcule ou on exprime l'une des inconnues en fonction de l'autre dans l 'une des équations  (1) ou (2) (isoler une inconnue à l'aide d'une des deux équations) pour obtenir une équation de premier degré à une seule inconnue 
Résoudre dans ℝ ² le système {\color{Red} \begin{cases}2x-y+1=0\ {\color{Blue} \ \ (1)}\\ 4x+y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
Exprimant y en fonction de x
\begin{cases}2x-y+1=0\\ 4x+y+3=0 \end{cases} \Leftrightarrow \begin{cases}-y=-1-2x\\ 4x+y+3=0 \end{cases}\Leftrightarrow \begin{cases}{\color{Blue} y=1+2x}\\ 4x+y+3=0 \end{cases}\\ \Leftrightarrow \begin{cases}{\color{Blue} y=1+2x}\\ 4x+{\color{Blue} (1+2x)}+3=0 \end{cases}\\ \Leftrightarrow \begin{cases}{\color{Blue} y=1+2x}\ \ \ {\color{Blue} (1)}\\ {\color{Red} 6x+4=0}\ \ \ {\color{Blue} (2)} \end{cases}
 il suffit donc de résoudre l'équation (2)  pour obtenir la valeur de x  et ensuite on remplace x par sa valeur dans l 'équation (1)pour obtenir la valeur de y
\begin{cases}{\color{Blue} y=1+2x}\ \ \ {\color{Blue} (1)}\\ {\color{Red} 6x+4=0}\ \ \ {\color{Red} (2)} \end{cases} \Leftrightarrow \begin{cases}{\color{Blue} y=1+2x}\ \ \ {\color{Blue} (1)}\\ {\color{Red} 6x=-4}\ \ \ {\color{Red} (2)} \end{cases} \Leftrightarrow \begin{cases}{\color{Blue} y=1+2x}\ \ \ {\color{Blue} (1)}\\ {\color{Red} x=\frac{-4}{6}=\frac{-2}{3}}\ \ \ {\color{Red} (2)} \end{cases}\\ \Leftrightarrow \begin{cases}{\color{Blue} y=1+2\left (\frac{-2}{3} \right )}\\ {\color{Red} x=\frac{-2}{3}} \end{cases} \Leftrightarrow \begin{cases}{\color{Blue} y=\frac{-1}{3}}\\ {\color{Red} x=\frac{-2}{3}} \end{cases}
On trouve le même résultat si on exprime  x en fonction de y\begin{cases}2x-y+1=0\\ 4x+y+3=0 \end{cases} \Leftrightarrow \begin{cases}2x=y-1\\ 4x+y+3=0 \end{cases}\Leftrightarrow \begin{cases}{\color{Blue} x=\frac{y-1}{2}}\\ 4x+y+3=0 \end{cases}\\ \Leftrightarrow \begin{cases}{\color{Blue} x= \frac{y-1}{2}}\\ {\color{Red} 3y-1=0} \end{cases} \Leftrightarrow \begin{cases}{\color{Blue} x=\frac{-2}{3}}\\ {\color{Red}y=\frac{-1}{3}}\end{cases}
En conclus que la solution du système est 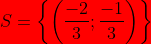S=\left \{\left ( \frac{-2}{3};\frac{-1}{3} \right ) \right \}
Interprétation graphique 
2 x - y +1= 0  s'écrit  aussi y = 2 x +1 c' est l'équation d'une droite 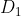 D_{1} 
( fonction affine  f(x) = 2 x + 1)
4 x + y +3 = 0 s'écrit  aussi y = - 4 x - 3 c' est l'équation d'une droite 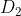D_{2}
( fonction affine  f(x) = - 4 x - 3)
La solution du système {\color{Red} \begin{cases}2x-y+1=0\\ 4x+y+3=0\end{cases}}
est le point \bg_white \large {\color{Blue} A\left ( \frac{-2}{3};\frac{-1}{3} \right )} l'intersection des deux droites \large {\color{DarkGreen} D_{1}} et  \large {\color{Red} D_{2}}
ii) Méthode de combinaison

Cette méthode  c'est de faire apparaître le même nombre de x ou de y dans les deux  équations ( on multiple chaque équation par un nombre afin que les coefficients de x ou de y soient les mêmes )
Résoudre dans ℝ ² le système {\color{Red} \begin{cases}2x-3y+1=0\ {\color{Blue} \ \ (1)}\\ 4x-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
ici on peut multiplier la première (1 ) équation par 2
\begin{cases}2x-3y+1=0\ {\color{Blue} \ \ (1)}\ \ {\color{Red} (\times 2)}\\ 4x-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases} \Leftrightarrow \begin{cases}{\color{Red} 4x}-6y+2=0\ {\color{Blue} \ \ (1)}\\ {\color{Red} 4x}-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases}
On soustrait membre à membre les deux équations (1) et (2) on obtient :
{\color{Magenta} -4y-1=0}\ donc \ {\color{Blue} y= \frac{-1}{4}}
On remplace y par 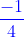{\color{Blue} \frac{-1}{4}} dans la deuxième (2) équation on obtient 4x -2\left ( \frac{-1}{4} \right )+3=0\Leftrightarrow 4x+\frac{7}{2}=0\ \ d'o\acute{u}\ \ \ {\color{Blue} x=\frac{-7}{8}}
En conclus que la solution du système   {\color{Red} \begin{cases}2x-3y+1=0\ {\color{Blue} \ \ (1)}\\ 4x-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
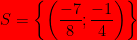
est S=\left \{ \left ( \frac{-7}{8} ;\frac{-1}{4} \right ) \right \}
Interprétation graphique:
2 x - 3 y +1= 0  s'écrit  aussi{\color{Blue} y=\frac{2}{3}x+\frac{1}{3}} c' est l'équation d'une droite  \bg_white \large {\color{Blue} D_{1}} 
  \left (fonction\ affine\ \ f(x)=\frac{2}{3}x+\frac{1}{3} \right )
4 x + 2 y +3 = 0 s'écrit  aussi {\color{Red} y=-2x-\frac{3}{2}} c' est l'équation d'une droite \bg_white \large {\color{Red} D_{2}}
\left (fonction\ affine\ \ f(x)=-2x-\frac{3}{2} \right )
La solution du système {\color{Red} \begin{cases}2x-3y+1=0\ {\color{Blue} \ \ (1)}\\ 4x-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
La solution du système {\color{Red} \begin{cases}2x-3y+1=0\ {\color{Blue} \ \ (1)}\\ 4x-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
est le point \bg_white {\color{DarkGreen} M\left ( \frac{-7}{8};\frac{-1}{4} \right ) } l'intersection des deux droites \bg_white \large {\color{Blue} D_{1}} et  \large {\color{Red} D_{2}}
Remarque:
On utilise  la méthode de substitution lorsque l’une des inconnues a pour coefficient 1 ou -1.
exemple 1){\color{Red} \begin{cases}2x-y+1=0\ {\color{Blue} \ \ (1)}\\ 4x+y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
On utilise, la méthode de combinaison dans tous les autres cas
 exemple 2){\color{Red} \begin{cases}2x-3y+1=0\ {\color{Blue} \ \ (1)}\\ 4x-2y+3=0\ {\color{Blue} \ \ (2)}\end{cases}}
iii)Méthode de Cramer 
Pour résoudre dans 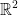\mathbb{R}^{2} un système d'équation  de type \bg_green\ {\color{Red}( S)}\ \begin{cases}ax+by=c\\ a'x+b'y=c'\end{cases}
On calcul le déterminant 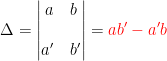\Delta=\begin{vmatrix}a\ \ \ b\\ \\ a'\ \ \ b' \end{vmatrix}={\color{Red} ab'-a'b}
1er cas 
Si {\color{Red} \Delta\neq 0} le système (S) admet  le couple ( x ; y) comme  seul solution tel que :
{\color{Red} x=\frac{\Delta x}{\Delta}}\ \ avec\ \ {\color{DarkRed} \Delta x= \begin {vmatrix}c\ \ \ b\\ \\ c'\ \ \ b'\end{vmatrix}}=cb'-c'b
{\color{Red} y=\frac{\Delta y}{\Delta}}\ \ avec\ \ {\color{DarkRed} \Delta y= \begin {vmatrix}a\ \ \ c\\ \\ a'\ \ \ c'\end{vmatrix}}=ac'-a'c donc S=\left \{ \left ( \frac{\Delta x}{\Delta} ;\frac{\Delta y}{\Delta} \right ) \right \}
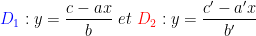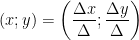
Interprétation graphique: les deux droites {\color{Blue} D_{1}}: y=\frac{c-ax}{b} \ et\ {\color{Red} D_{2}} :y=\frac{c'-a'x}{b'}sont sécantes ,l'intersection de \bg_white \large {\color{Blue} D_{1}}et  \bg_white \large {\color{Red} D_{2}} est le point (x;y)= \left ( \frac{\Delta x}{\Delta} ;\frac{\Delta y}{\Delta} \right )
Exemple :
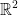
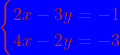
résoudre dans \mathbb{R}^{2} \bg_blue {\color{DarkOrange} \begin{cases}2x-3y=-1\\ 4x-2y=-3\end{cases}}
\Delta=\begin{vmatrix}2\ \ \ -3\\ \\ 4\ \ \ -2 \end{vmatrix}={\color{Red} -4+12}=8\neq 0 le systeme   \bg_blue {\color{DarkOrange} \begin{cases}2x-3y=-1\\ 4x-2y=-3\end{cases}} admet une seule solution ( x;y ) tel que{\color{Red} x=\frac{\Delta x}{\Delta}}\ \ avec\ \ {\color{DarkRed} \Delta x= \begin {vmatrix}-1\ \ \ -3\\ \\-3\ \ \ -2\end{vmatrix}}=-7\Rightarrow{\color{Red} x=\frac{-7}{8}}
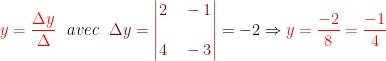
et  {\color{Red} y=\frac{\Delta y}{\Delta}}\ \ avec\ \ {\color{DarkRed} \Delta y= \begin {vmatrix}2\ \ \ -1\\ \\ 4\ \ \ -3\end{vmatrix}}=-2\Rightarrow {\color{Red} y=\frac{-2}{8}=\frac{-1}{4}}
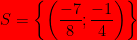
donc  S=\left \{ \left ( \frac{-7}{8} ;\frac{-1}{4} \right ) \right \}
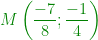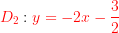
le point \bg_white {\color{DarkGreen} M\left ( \frac{-7}{8};\frac{-1}{4} \right ) } l'intersection des deux droites \bg_white \large {\color{Blue} D_{1}}: {\color{Blue} y=\frac{2}{3}x+\frac{1}{3}} et  \bg_white \large {\color{Red} D_{2}}: {\color{Red} y=-2x-\frac{3}{2}}
2eme cas
{\color{Red} Si\ \Delta=0} et {\color{DarkRed} \Delta x=0} et {\color{DarkRed} \Delta y=0} le système \bg_green\ {\color{Red}( S)}\ \begin{cases}ax+by=c\\ a'x+b'y=c'\end{cases} admet une infinité de solution donc :
\bg_red S=\left \{ (x;y)\in \mathbb{R}^{2}/y=\frac{c-ax}{b} \right \}
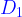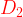Interprétation graphique: les deux droites \bg_white \large {\color{Blue} D_{1}}et \bg_white \large {\color{Red} D_{2}} ont la même équation  , donc elles  sont confondues.
Exemple :
résoudre dans 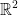\mathbb{R}^{2}\bg_green\ \begin{cases}x+y=-1\\ 2x+2y=-2\end{cases}
on a Δ= (1 × 2) - ( 2 × 1 ) = 0   
Δx = ( - 1 × 2) - ( - 2 × 1 )= 0
Δy = ( 1 × (-2) ) - ( 2 × (-1) ) =0
Puisque Δ = 0 et Δx = 0 et Δy = 0  donc  \bg_red S=\left \{ (x;y)\in \mathbb{R}^{2}/y=-1-x\right \}
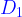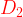les deux droites \bg_white \large {\color{Blue} D_{1}} et \bg_white \large {\color{Red} D_{2}} ont la même équation 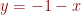{\color{DarkRed} y=-1 -x} donc elles  sont confondues.


3eme cas
{\color{Red} Si\ \Delta=0} et \left ({\color{DarkRed} \Delta x\neq 0}\ ou \ {\color{DarkRed} \Delta y\neq 0} \right )  le système \bg_green\ {\color{Red}( S)}\ \begin{cases}ax+by=c\\ a'x+b'y=c'\end{cases} n'admet pas de solution dans \mathbb{R}^{2} donc  S = ∅
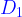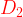Interprétation graphique: les deux droites \bg_white \large {\color{Blue} D_{1}}et \bg_white \large {\color{Red} D_{2}} ont  même coefficient directeur   ,et elles  sont parallèles
Exemple :
Résoudre dans ℝ ²   
on a Δ= (1 × 2) - ( 2 × 1 ) = 0   
Δx = ( - 1 × 2) - ( - 1 × 1 )= - 1 
Δy = ( 1 × (-1) ) - ( 2 × (-1) ) = 1
Puisque Δ = 0 et Δx ≠ 0 et Δy ≠ 0  donc  S = ∅
Interprétation graphique:
la droite 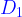\bg_white \large {\color{Blue} D_{1}} d'équation y = -x -1  et la droite 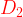\bg_white \large {\color{Red} D_{2}} d'équation y = -x  -1/2  sont sont parallèles





هل اعجبك الموضوع :

أخر المواضيع من قسم : Lycée

Commentaires

Enregistrer un commentaire