Exemple:
La définition est :
la racine carré d'un nombre a est un nombre dont le carré vaut a :
Propriété:
Quel que soit a nombre réel positif
Exemple:
Opérations sur les racines carrées:
Somme et différences de racines carrées:Exemples :
1) calculons :
on a :
On remarque que :
2) calculons :
on a:
on remarque aussi que :
3) calculons :
on a:
ce qui montre que :
4) calculons:
on a :
montre que :
Donc:
Dans le cas général, il n'existe pas de formule avec l'addition et la soustraction
Produits et puissances de racines carrées:
Théorème:
le produit de deux racines carrées est égale à la racine carrée du produit
Démonstration;
Remarque : pour
En général racine carrée de a est égale à valeur absolue de a:
exemples:
calculer :
simplifier:
calculer :
Déduction
pour :
Quotients de deux racines carrées
Théorème:
Le quotient de deux racines carrées est égale à la racine carrée du quotient
Démonstration:
exemple:
calculer
Supprimer la racine carrée au dénominateur
Pour calculer facilement les valeurs approchées c'est préférable d'avoir les radicaux au numérateur qu'au dénominateur pour cette raison on utilise propriété 1 ou propriété 2
Propriété 1:
pour
Propriété 2:
Exemples :
1) Supprimons la racine carrée au dénominateur :
2) Supprimons la racine au dénominateur :
3) Supprimer la racine carrée au dénominateur en utilisant le conjugué du dénominateur
exemple: 1
exemple 2:
Résoudre l 'équation :
Définition:
Exemples:
Résoudre l'équation: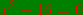
d'une autre façon :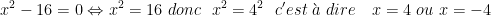
L'équation: 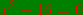 admet deux solutions :
admet deux solutions :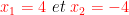




Commentaires
Enregistrer un commentaire