1)Rappels:
L'ensemble des nombres réels noté 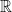 est une droite numérique , cette droite munie d'une origine O et d'un vecteur
est une droite numérique , cette droite munie d'une origine O et d'un vecteur 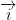 tel que
tel que
A tout point M de cette droite correspond un unique nombre x appelé réel tel que 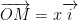
A tout nombre réel x correspond un point M de cette droite tel que 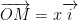
les nombres à droite de O (nombre 0) sont les réels positifs c'est l 'ensemble 
les nombres à gauche de O (nombre 0) sont les réels négatifs c'est l 'ensemble 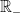
Remarque :
Un nombre réel qui n'est pas rationnel est dit irrationnel
exemple:
2)Opérations sur l'ensemble des réels:
1)addition et multiplicationi)Somme
Soient a, b et c des nombres réels
a + b = b + a l 'addition est commutative dans
(a + b) + c = a + ( b +c ) l 'addition est associative dans
a + 0 = 0 +a = a : 0 est l'élément neutre pour l 'addition dans
a - a =0 : -a est le symétrique de a pour l 'addition
ii) produit
a× b = b × a la multiplication est commutative dans
a× ( b × c) =( a × b ) × c : la multiplication est associative dans
a × 1 = 1× a = a : 1 est l élément neutre pour la multiplication dans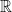
a × 0 = 0 : 0 est l 'élément absorbant dans la multiplication
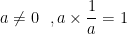 : a est l' inverse de
: a est l' inverse de 
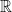
a + b = c ⇔ a = c - b
Soient ( a; c) ∈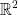 et ( b; d)∈
et ( b; d)∈ :
: 
Soit a ∈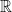 et soit (c ; b )∈
et soit (c ; b )∈ :
: 
Soit ( a ; b ) ∈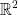 et soit c ∈
et soit c ∈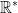 :
: 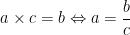
Soient ( a; c) ∈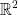 et ( b; d)∈
et ( b; d)∈ :
: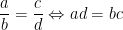
 démonstration clic ici
démonstration clic ici
 v
v
Soient ( a;b) ∈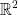 et ( b; c ; d ) ∈
et ( b; c ; d ) ∈ 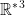 :
: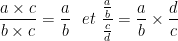

1)Utilisation du triangle de pascal pour les identités remarquables:
On débute avec tout l 'exposant sur a et 0 sur b ,puis à chaque terme on diminue l'exposant de a et on augmente celui de b jusqu'à ce que l'exposant de a est 0
On sait que :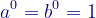
L'intersection de la ligne n et de la colonne p représente le coefficient de rang p ( c'est le coefficient binomial)
a × 0 = 0 : 0 est l 'élément absorbant dans la multiplication
3)Règles de calcul dans 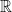
Soient a , b et c les élément de a + b = c ⇔ a = c - b
Soient ( a; c) ∈
Soit a ∈
Soit ( a ; b ) ∈
Soient ( a; c) ∈
Soient ( a;b) ∈
4)Identités remarquables
1)Utilisation du triangle de pascal pour les identités remarquables:
On débute avec tout l 'exposant sur a et 0 sur b ,puis à chaque terme on diminue l'exposant de a et on augmente celui de b jusqu'à ce que l'exposant de a est 0
On sait que :
L'intersection de la ligne n et de la colonne p représente le coefficient de rang p ( c'est le coefficient binomial)
Exemples:

2)Règles
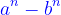 est toujours divisible par (a – b)
est toujours divisible par (a – b)





 trouver les valeurs de a , b , c et d si
trouver les valeurs de a , b , c et d si 




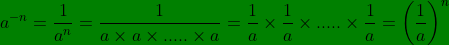
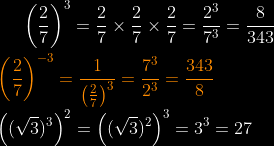
4)Puissance de 10:
n∈ ℕ*:
5)Ecriture scientifique d'un nombre : manière d'écriture des nombres très petits ou très grands
Quel que soit le nombre décimal positif x peut s'écrit sous forme
si x est négatif l'écriture scientifique est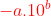
Exemple :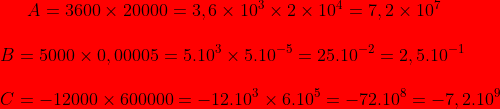


2)Règles
1) Pour 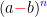 il faut mettre un signe - devant chaque terme où b a pour exposant un nombre impaire
il faut mettre un signe - devant chaque terme où b a pour exposant un nombre impaire
Exemple :
2) 
Le développement de 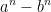 selon la valeur de n , avec mise en évidence des facteurs en ( a + b) et ( a- b)
selon la valeur de n , avec mise en évidence des facteurs en ( a + b) et ( a- b)
Exemples:
3)Si n est impair : 
exemple:
4)Si b=1 :
Exemple: et aussi
et aussi 
Exercice d’application:
factoriser les expressions suivantes:
développer l'expression suivante:
solution:
factorisation :
Exercice :Développer l'expression suivante
5)Puissance d'une racine carrée:
1)Rappel : la racine carré définition clic ici
2)Puissance d'une racine carrée
Soient x∈ ℝ* et n∈ ℕ*:
3Propriétés:
Exemples:4)Puissance de 10:
n∈ ℕ*:

5)Ecriture scientifique d'un nombre : manière d'écriture des nombres très petits ou très grands
Quel que soit le nombre décimal positif x peut s'écrit sous forme
si x est négatif l'écriture scientifique est
Exemple :




Commentaires
Enregistrer un commentaire