المتجهات

1) التعريف

المتجهة هي نصف مستقيم موجه والذي يمثل كمية اوسرعة او قوة , نحدد كل متجهة بثلالة عناصر الاتجاه, المقدارونقطة التاثير اي نقطة الانطلاق و نرمز المتجهة ب $\overrightarrow{v}$

2) تساوي متجهاتين

نقول ان المتجهتين متساويتان اذا كان لهما نفس الاتجاه و نفس المنحى و نفس المقدارو بصغة اخرى تكون المتجهات متساوية اذا تساوت احداثياتهما

3) جمع المتجهات

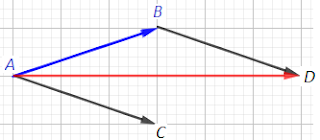
لنرسم النقطة D حيث $\bg_white {\color{Blue} \overrightarrow{AD}}= \overrightarrow{AB}+ \overrightarrow{AC}$ و $\overrightarrow{AC}= \overrightarrow{BD}$

$\overrightarrow{AC}+ \overrightarrow{AB}= \overrightarrow{AB}+ \overrightarrow{BD}=\overrightarrow{AD}$

مجموع المتجهتين 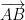$\overrightarrow{AB}$ و $\overrightarrow{AC}$ هو المتجهة $\overrightarrow{AD}$ بحيث ABCD يشكل متوازي الأ ضلاع

4) علاقة شال

قاعدة:

اذا كانت A وB و C نقط من المستوى فان : $\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}$

قاعدة متوازي الأضلاع $\overrightarrow{OA}+ \overrightarrow{OB}= \overrightarrow{OM}$

5) ضرب متجهة في عددحقيقي

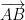انشيء النقطة C بحيث $\overrightarrow{AC}=3 \overrightarrow{AB}$

انشيء النقطة E بحيث $\overrightarrow{AE}=-2 \overrightarrow{AB}$

$\overrightarrow{AC}$ و $\overrightarrow{AB}$ لهما نفس المنحى لأن3 موجب

$\overrightarrow{AE}$ و $\overrightarrow{AB}$ لهما منحيان منعاكسان لأن 2- سالب

* تعريف
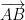$\overrightarrow{AB}$ متجهة غير منعدمة و k عدد حقيقي نقول ان المتجهة $\overrightarrow{AC}$ هي جداء المتجهة $\overrightarrow{AB}$ في العدد k

اذا كانت C من المستقيم (AB) حيث $\overrightarrow{AC}=k\overrightarrow{AB}$

- اذا كان k موجب فان 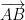$\overrightarrow{AB}$ و $\overrightarrow{AC}$ لهما نفس المنحى

-اذا كان k سالب فان $\overrightarrow{AB}$ و $\overrightarrow{AC}$ لهما منحيان منعاكسان

مثال

لتكون $\overrightarrow{u}$ و $\overrightarrow{v}$ و $\overrightarrow{w}$ 3 متجهات حيث $\overrightarrow{v}=3\overrightarrow{u}$ و $\overrightarrow{w}=-2\overrightarrow{u}$

$\overrightarrow{u}$ و $\overrightarrow{v}$ و $\overrightarrow{w}$ لهم نفس المنحى (منحى $\overrightarrow{u}$ ) . $\overrightarrow{u}$ و $\overrightarrow{v}$ لهما نفس الاتجاه .

$\overrightarrow{u}$ و $\overrightarrow{w}$ لهما اتجاه معاكس

مقدار او القمة المطلقة ل $\overrightarrow{v}$ هو 3 مقدار $\overrightarrow{u}$ اي $\left \| \overrightarrow{3u} \right \|=3 \left \| \overrightarrow{u} \right \|$

مقدار او القمة المطلقة ل $\overrightarrow{w}$ هو 2 مقدار $\overrightarrow{u}$ اي $\left \| \overrightarrow{-2w} \right \|=2 \left \| \overrightarrow{u} \right \|$

** خاصيات

خاصية 1

اذا كان $\overrightarrow{AC}=k\overrightarrow{AB}$ فان A و B و C نقط مستقيمية

خاصية 2

انشيء المتجهة $\overrightarrow{MN}$ بحيث $\overrightarrow{MN}=2\overrightarrow{EF}$

و بما أن $\overrightarrow{MN}=2\overrightarrow{EF}$ نقول ان $\overrightarrow{MN}$ و $\overrightarrow{EF}$ مستقيميان

اذا كان $\overrightarrow{MN}=k\overrightarrow{EF}$ فان المستقيمان (MN) و (EF) متوازيان

خاصية3

لتكو ن $\overrightarrow{u}$ و $\overrightarrow{v}$ متجهتان معينتان و k عدد حقيقي :

$k\overrightarrow{u}=0$ يعني k=0 او0= $\overrightarrow{u}$

$k(\overrightarrow{u}+\overrightarrow{v})=k\overrightarrow{u}+k\overrightarrow{v}$
6) الازاحة

'M هي صورة M بالازاحة $t_{\overrightarrow{u}}$

$t_{\overrightarrow{u}} \rightarrow (M)=M'$ يعني $\overrightarrow{AB}= \overrightarrow{MM'}$ اي أ ن 'ABMM متوازي الأضلاع

تعريف

A وB و M نقط من المستوى تكون 'M صورة M بالازاحة $t_{\overrightarrow{u}}$ التي تحول A الى B يعني $\overrightarrow{AB}= \overrightarrow{MM'}$ اذا كان

للمستقيمين (AB) و ('MM) نفس الاتجاه

المنحى من M نحوى N هو المنحى من A نحوىB
مقدار او المسافة 'AB= MM
7) خاصيات

بما أن $\bg_white t_{\overrightarrow{u}} \rightarrow (E)=F$ فان $\bg_white \overrightarrow{u}= \overrightarrow{EF}$

بما أ ن $\bg_white t_{\overrightarrow{u}} \rightarrow (G)=H$ فان $\bg_white \overrightarrow{u}= \overrightarrow{GH}$ و بالتالي فان $\bg_white \overrightarrow{EF}= \overrightarrow{GH}$ و GE= HF
خاصية 1: F و H صورتا E و G على التوالي بالازاحة يعني ان EFGH متوازي الأضلاع و GE= HF
صورة مستقيم:
بما أن $\bg_white t_{\overrightarrow{u}} (M)=N$ و $\bg_white t_{\overrightarrow{u}} (G)=H$ فان $\bg_white \overrightarrow{MG}= \overrightarrow{NH}$ و MN = GH h اذن (MG) // (NH)
خاصية 2 : صورة مستقيم بازاحة هو مستقيم يوازيه
صورة قطعة :

بما أ ن $\bg_white t_{\overrightarrow{u}} (M)=E$ و $\bg_white t_{\overrightarrow{u}} (N)=F$ فان MN = EF و [MN] =[EF]

خاصية 3 : صورة قطعة بازاحة هي قطعة تقايسها

صورة نصف مستقيم بازاحة هو نصف مستقيم يوازيه

صورة زاوية

$\begin{cases} t_{\overrightarrow{u} (O)=O'\\ t_{\overrightarrow{u} (A)=A'\\ t_{\overrightarrow{u} (B)=B' \end{cases}$ اذن $t_{\overrightarrow{u}} (A\^\O B)= A'\^\O' B'$

خا صية 4 : صورة زاوية بازاحة هي زاوية تقايسها

صورة دائرة

$\overrightarrow{u}$ متجهة معينة و(C( O; r دائرة مركزها O و شعاعها r و M نقطة من الدائرة

(C( O ; r

لنشيء النقط 'O و 'M صورتي O و M على التوالي بالازاحة $t_{\overrightarrow{u}}$

$t_{\overrightarrow{u}} (O)= O'$ و $\bg_white t_{\overrightarrow{u}} (M)= M'$ اذن $\bg_white \overrightarrow{OM}= \overrightarrow{O'M'}$ و 'OM= O'M و بالتالي 'r = r