Ecriture fractionnaire

1-Ecriture fractionnaire الكتابة الكسرية

Définition :

a et b deux nombres décimaux avec b≠0; $\frac{a}{b}$

est le quotient de a par b : $\frac{a}{b}=a\div b$

On dit que $\frac{a}{b}$ est une écriture fractionnaire du quotient a÷b

a est le numérateur et b le dénominateur

si a et b sont deux entiers naturel avec b≠0 on dit que $\frac{a}{b}$
est une fraction

تعريف :

a و b عددين عشريين مع b ≠ 0 ؛ $\frac{a}{b}$ هو حاصل قسمة a على b $\frac{a}{b}=a\div b$

نقول أن $\frac{a}{b}$ هي كتابة كسرية للحاصل a÷b a : هو البسط و b المقام

إذا كان a و b رقمين طبيعيين مع b ≠ 0 فإننا نقول أن $\frac{a}{b}$ هو عدد كسري

Exemple :

$\bg_white \frac{3}{6}$ Est une écriture fractionnaire et 3÷6=0,5 est un nombre décimal

$\bg_white \frac{3}{6}$ عبارة عن كتابة كسرية و 0.5 =6 ÷ 3 عدد عشري

$\frac{4,4}{1,1}$ Est une écriture fractionnaire et $4,4\div 1,1=\frac{4,4}{1,1}=\frac{44}{11}={\color{Magenta} 4}$ est un nombre entier naturel

$\frac{4,4}{1,1}$ عبارة عن كتابة كسرية و $4,4\div 1,1=\frac{4,4}{1,1}=\frac{44}{11}={\color{Magenta} 4}$ عدد صحيح طبيعي

$\frac{2}{3}$ Est une écriture fractionnaire et $2\div 3={\color{Magenta} 0,6666666}$ n’est pas un nombre décimal

$\frac{2}{3}$ هو كتابة كسرية و $2\div 3={\color{Magenta} 0,6666666}$ ليس بعدد عشري

Remarque : une fraction peut être nombre décimal ; un nombre entier naturel et aussi ne pas être nombre décimal

comme $\frac{2}{3}$ n'est pas décimal car la division 2 par 3 ne s’arrête jamais

2-Comparaison des nombres en écriture fractionnaireمقارنة الاعداد الكسرية

* cas ou les dénominateurs sont les mêmes الحالة التي تكون فيها المقامات (القواسم) متطابقة

Propriété :

Si deux fractions ont le même dénominateur alors la plus grande est celle qui a le plus grand numérateur

خاصية

لمقارنة عددين كسريين لهما نفس المقام الاكبر هو الذي لديه أكبر بسط

Exemple :

car le dénominateur est le même pour les deux fractions et 9,3< 17

نفس المقام و 9,3< 17

**cas ou les numérateurs sont les mêmesالحالة التي يكون فيها البسط متطابق

Propriété

Si deux fractions ont le même numérateur alors la plus grande est celle qui a le plus petit dénominateur

خاصية

مقارنة عددين كسريين لهما نفس البسط الاكبر هو الذي لديه أصغر مقام

Exemple :

car le numérateur est le même pour les deux fractions et 3< 7

لأن العدد ين لهما نفس البسط و 3< 7

***cas ou les dénominateurs sont différents الحالة التي تكون فيها المقامات (القواسم) مختلفة

Propriété

Dans ce cas on écrit les deux (réduire en même dénominateur les deux fractions) fractions avec même dénominateur

خاصية

في هذه الحالة نكتب الكسرين بنفس المقاماي نواحد المقام للعددين

Exemple :

Comparant 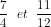$\frac{7}{4} \ \ et\ \ \frac{11}{12}$

On sait que 12= 4×3 donc 12 est un multiple de 4 alors

Maintenant on compare

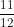$\frac{28}{12} \ \ et\ \ \frac{11}{12}$ fractions ayant même dénominateur et puisque 28>11 donc

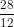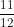لنقارن $\frac{7}{4}$ و $\frac{11}{12}$ نعلم أن3×4=12 هو من مضاعفات العدد 4 ادن الان نقارن العددين $\frac{28}{12}$ و $\frac{11}{12}$ كسريان لهما نفس المقام و بما أن 11<28 ادن

****Comparer des fractions à 1 : مقارنة عدد كسري ب1

Propriété
Si a< b alors $\frac{a}{b}$ est plus petit que 1

Si a> b alors $\frac{a}{b}$ est plus grand que 1

خاصية
إذا كانتa <b، فإن $\frac{a}{b}$ أصغر من 1

إذا كانت a> b فإن $\frac{a}{b}$ أكبر من 1

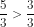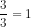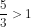
Exemple:1) 5 > 3 donc $\frac{5}{3}> \frac{3}{3}$ et puisque $\frac{3}{3}=1$ alors $\frac{5}{3}> 1$

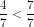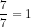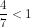
2) 4 < 7 donc $\frac{4}{7}< \frac{7}{7}$ et puisque $\frac{7}{7}=1$ alors $\frac{4}{7}< 1$

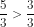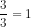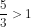
1) 5 > 3 ادن $\frac{5}{3}> \frac{3}{3}$ و بما أن $\frac{3}{3}=1$ ادن $\frac{5}{3}> 1$

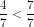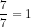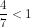
2) 4 < 7 ادن $\frac{4}{7}< \frac{7}{7}$ و بما أن $\frac{7}{7}=1$ ادن $\frac{4}{7}< 1$

3- comment trouver un dénominateur commun :كيفية العثور على قاسم مشترك

Pour trouver un dénominateur commun (ou plus !) à deux fractions, on écrit les multiples de chaque dénominateur pour trouver un multiple commun qui est dans les deux listes.

Bien souvent, on choisit le plus petit pour simplifier les calculs.

للعثور على قاسم مشترك لكسرين (أو أكثر!)، نكتب مضاعفات كل قاسم لإيجاد مضاعف مشترك في كلتا القائمتين

، لكن غالبًا ما نختار الأصغر لتبسيط العمليات الحسابية.

Voir vidéo شاهد الفيديو

Exemple:

Réduire au même dénominateur les fractions :c'est à dire Trouver un dénominateur commun àLes dénominateurs sont 8 et 10 On écrit leurs multiples

les multiples de 8 sont: 8; 16; 24; 32; 40; 48; 56; 64; 72; 80;.......

les multiples de 10 sont: 10; 20; 30; 40; 50; 60; 70; 80; 90; 100…………

40 et 80 sont deux multiples communs de 8 et 10 (on trouve aussi d'autres si on continue la liste des multiples)

Mais bien souvent, on choisit le plus petit pour simplifier les calculs.

le plus petit multiple commun de 8 et 10 est 40 : c'est le plus petit dénominateur commun pour les fractions

Maintenant écrire les deux fractions, dont le dénominateur est 40 $\bg_white \frac{9}{8}=\frac{9\times 5}{8\times 5}=\frac{45}{{\color{red} 40}}\ et\ \ \frac{3}{10}=\frac{3\times 4}{10\times 4}=\frac{12}{{\color{Red} 40}}$

واحد المقام ل:اي العثور على مضاعف مشترك للعددين 8 و10

مضاعفات 8 هي : 8 ; 16 ; 24 ; 32 ; 40 ; 48 ; 56 ; 64 ; 72 ; 80;........

مضاعفات 10 هي : 10; 20; 30; 40; 50; 60; 70; 80; 90; 100;........

40 و 80 هما المضاعفان المشتركان بين 8 و 10(نجد أيضًا غيرها إذا واصلنا قائمة المضاعفات)

لكن غالبًا ما نختار الأصغر لتبسيط العمليات الحسابية.

المضاعف المشترك الاصغر للعددين 8 و 10هو 40 اي القاسم ( المقام) المشترك الأصغر للكسريان

الآن نكتب بمقام مشترك 40

$\bg_white \frac{9}{8}=\frac{9\times 5}{8\times 5}=\frac{45}{{\color{red} 40}}$ و $\frac{3}{10}=\frac{3\times 4}{10\times 4}=\frac{12}{{\color{Red} 40}}$

voir aussi Multiplication de deux fractions جداء عددين كسريي

الرياضيات

القائمة الرئيسية

الصفحات

Ecriture fractionnaire

أخر المواضيع من قسم : 1ère Année Collège

Commentaires

Enregistrer un commentaire