Projection

1- projection d 'un point sur une droite

2-projection orthogonale sur une droite du plan

3- Théorème de Thalès: sens direct et sens réciproque (sens inverse)

4- Conservation du coefficient de colinéarité de deux vecteurs

1- projection d 'un point sur une droite

soient (D) et (Δ ) deux  droites  sécantes et soit A un point  quelconque du  plan .La projection sur la droite (D) selon la direction (Δ ) transforme le point A en un  point A' tel que
 A' est sur une droite  Δ' (AA') parallèle  à  (Δ)
A' est sur la droite (D)
donc (D) et  Δ' se rencontrent  en un point unique A'  
le point A' est la projection du point A sur la droite (D)  parallèlement à Δ  
A' ∈ D  est le projeté d'une infinité de points ,ces points représentent une droite Δ'(AA') parallèle à Δ

Définition :
Soient (D) et (Δ )deux droites sécantes et  A un point du plan tel que A∉ (D)
Le point A' est la projection du point A sur la droite (D )parallèlement  à (Δ) c est à dire A'∈ (D )et la droite (AA') parallèle à (Δ) ( Δ'// Δ) on dit que A' est le projeté de A sur la droite D parallèlement  à (Δ) .On le note P(A)=A'   P est appelé projection sur (D) parallèlement  à (Δ)
Exemple d' application
A' est le projeté de point A sur la droite (D) parallèlement  à (Δ)
A' est le projeté des points  A , M, N et P sur la droite (D) parallèlement  à (Δ)
E est le projeté de point E sur la droite (D) parallèlement  à (Δ)
le segment [ A'B'] est le projeté  du segment [AB]  sur la droite (D) parallèlement  à (Δ)
B' est le projeté de point B sur la droite (D) parallèlement  à (Δ)
C' est le projeté de point C sur la droite (D) parallèlement  à (Δ)

Remarque :
si le point A ∈ (D), il est son propre projeté

la projection du point A sur la droite (D) parallèlement  à (Δ) ne change pas si  on remplace la droite  (Δ) par une autre  droite  parallèle à (Δ) 

2-projection orthogonale sur une droite du plan
Définition:
Soient (D) et (Δ) deux droites perpendiculaire sur le plan 
A' est  le  projeté du point A sur la droite (D) parallèlement à (Δ)
le point A' est appelé la projection orthogonale du point A sur la droite  (D)

3- Théorème de Thalès: sens direct et sens réciproque :

a)Théorème Thalès sens direct 

soient (D) et (Δ) deux droites sécantes en point A  sachant que  les points A , B  et C  appartiennent  à (D) et A , M , et N appartiennent à (Δ) et aussi (BM) // (CN) comme le montre la figure ci dessous:

Dans les trois cas on a : 

- les trois points A, B et C sont alignés

- les trois points  A , M et N sont alignés

- les droites (B M) et (C N) sont parallèles  : (B M) // (C N) et d' après le théorème du Thalles :

On a :tel que  k est le même  nombre réel  pour ces égalités

alors en déduit que :

Exemples:

Soit (ABC) un triangle et (I J)  // (B C) voir figure ; tel que A J= 6 et A I = 12  et AC = 34 et AB = x

calculons la valeur de x

Par hypothèse on  (I J)  // (B C) 

d' après le théorème  direct du Thalès  on a :

propriété 1:

soient deux droites (D) et (Δ) sécantes en A  et  

 soient B  et C deux points de ( D)  différent de A 

soient  M et N deux point de (Δ) différent de A

si (B M) // (C N)  alors :

Théorème de Thalès projection directe

propriété 2:

soient (D) et (K) deux droites sécantes et (Δ) sécante à les deux droites (D) et (K)

soient A  et B deux point appartiennent à (K) si C∈ (K) et A', B'et C'  les projections respectivement de  A, B et C sur la droite (D) parallèlement à (Δ) alors 

b)Théorème de Thalès sens  inverse

Exemple:

soient (D) et (Δ) deux droites sécantes en point A  tel que:

 les points A ,B et M  appartiennent  à (D) 

 les points A , C  et N  appartiennent  à (Δ) .Comme le montre les figures suivantes: 

On remarque  que dans les trois cas :

et par suite ( k est le même  nombre réel  pour ces égalités)

en déduit donc que (MN) // ( B C)

Propriété 3:

soient deux droites (D) et (Δ) sécantes en A  et  

 soient B  et M deux points de ( D)  différent de A 

soient  N et C deux point de (Δ) différent de A

Si les points A et M et B et les points A et N et C  alignés dans le même ordre

 et 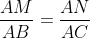alors  les droites (MN) et (B C) sont parallèles 

Exemple :

Soit ABC un triangle tel que:( voir figure)

- (AB) et (AC) se rencontrent en  A 

-AD=18 et AB=6 et CE= 18 et A E=27

montrons que  (B C) //( E D)

Par hypothèses on a : les points A et B et D et les points A et C et E  alignés dans le même ordre

AC=A E - CE = 27 - 18 = 9  donc  et d’après Théorème inverse de Thalès  en conclus que (B C) // (E D)

Remarque :

Ils faut toujours tenir compte de l 'ordre de l'alignement des points sur une droite 

dans l'exemple suivant : Mais (MN) et (B C) ne sont pas parallèles

4- Conservation du coefficient de colinéarité de deux vecteurs:

 rappel:

On dit que deux vecteurs  et  sont colinéaires lorsqu' ils ont même direction Si   et sont colinéaires  alors   =k   ( k un nombre réel)

Propriété 4:

Soient deux droites (D) et (Δ) sécantes en I et  et  deux vecteurs tel que  = k 

Si A' , B' , M'  et N'  les projections (respectivement) de A , B , M et N  sur la droite (D) parallèlement (Δ) alors 

Exemple d' application:

Soit un triangle ABC   et  M ∈ (B C ) et  N milieu du segment [AC]  tel que ;et soit P le point de rencontre de la droite (AC) et la parallèle à (B N )  qui passe  par le point M

vérifiant que  

Par hypothèse  on (P M) // (N B) donc les points N  , P et C sont les projections  respectivement  des points B , M et C  sur la droite (A C ) parallèlement  à  la droite ( N B)

et puisque  et  la projection conserve le  coefficient de colinéarité de deux vecteurs alors  par suite