un ensemble est un assemblage ou collection d'élément spécifiques que l 'on note par A; B; C; E......
Exemples:
E={ 2,3, 4, 5, 6 ,7 ,8 ,9 ,10 ,11 12,13} A= { 1,2 ,3} ℕ={0,1,2,3,4,5,6..........}
On peut définir un ensemble par E={x ∈ ℕ / 2 ≤ x ≤13 } ;
ℕ l’ensemble de tous les nombres entiers positifs : ℕ ={ x ∈ ℕ / x ≥ 0 }
Cas particulier:
L' ensemble ne contenant aucun élément est appelé l 'ensemble vide et noté ∅
L'ensemble qui contient un seul élément est appelé singleton exemple :
B= {1}
2) Exercices d 'application :
1)On considère l'ensemble suivant 
écrire E en extension(c'est-à-dire donnant tous les éléments de E)
2) soit B= { (x,y) ∈ℤ ² / x² + x y - 2 y² = - 5}
i) vérifier que : x² + x y - 2 y² = ( x - y)( x + 2 y)
i i) écrire B en extension
3- Appartenance :
Soit E un ensemble non vide c'est à dire comprend des élément si a est un élément de l'ensemble E, on dit que a appartient à E .On le note : a ∈ E
si a n 'appartient pas à E , on le note a ∉ E
Exemples:
1 est un élément de l 'ensemble des entiers naturels ℕ , on note 1 ∈ ℕ
√2 n' est pas un élément de l'ensemble des nombres rationnels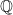
, on note 
√2 est un élément de l' ensemble des nombres réels ,on note √2 ∈ℝ
4) Inclusion:
soient E et A deux ensembles on dit que l'ensemble A est inclus dans l 'ensemble E si tout élément de A appartient à E on le note A⊂ E
On lit : A⊂ E : A est inclus dans l'ensemble E OU A est une partie de l'ensemble E OU A est contenu dans l'ensemble E OU A est un sous ensemble de l'ensemble E
Soient A et B deux parties de E (A⊂ E et B⊂ E )
i)A est contenu dans l'ensemble B c'est à dire A⊂ B autrement dit:
"(A⊂ B)⇔ (∀ x∈ E):x∈ A⇒ x∈ B"
Soit E un ensemble non vide c'est à dire comprend des élément si a est un élément de l'ensemble E, on dit que a appartient à E .On le note : a ∈ E
si a n 'appartient pas à E , on le note a ∉ E
Exemples:
1 est un élément de l 'ensemble des entiers naturels ℕ , on note 1 ∈ ℕ
√2 n' est pas un élément de l'ensemble des nombres rationnels
√2 est un élément de l' ensemble des nombres réels ,on note √2 ∈ℝ
4) Inclusion:
soient E et A deux ensembles on dit que l'ensemble A est inclus dans l 'ensemble E si tout élément de A appartient à E on le note A⊂ E
On lit : A⊂ E : A est inclus dans l'ensemble E OU A est une partie de l'ensemble E OU A est contenu dans l'ensemble E OU A est un sous ensemble de l'ensemble E
Soient A et B deux parties de E (A⊂ E et B⊂ E )
i)A est contenu dans l'ensemble B c'est à dire A⊂ B autrement dit:
"(A⊂ B)⇔ (∀ x∈ E):x∈ A⇒ x∈ B"
ii) A n'est pas contenu dans l'ensemble B s'il existe un élément de E appartient à A et n'appartient pas à B on le note A ⊄ B
"(A ⊄ B) ⇔ (∃ x∈ E):x∈ A et x∉ B"
Exemples : ℕ *⊂ ℕ ; ] 0, 1[ ⊄ 
( car 
] 0,1[ et 
)
Propriétés:
Soient A .B et C trois parties de l'ensemble E:
1) A⊂ A ; 2) ∅ ⊂ A ; 3) (A⊂ B et B ⊂ A )⇔ A=B ; 4)(A⊂ B et B ⊂ C )⇒ A⊂ C
Remarque:
{e , f } ={f , e} les deux ensembles contient les mêmes éléments
5) Exercices d 'application :
1) Soit 
2)verifier que 
3)montrer que A ⊂ [ 0,1] et est ce que [ 0,1]⊂A
4) soient 
montrer que E=F .
Commentaires
Enregistrer un commentaire