Vecteurs

1) Définition
2) Norme d'un vecteur
3)Egalité de deux vecteurs
4)Somme de deux vecteurs
5)Multiplication d'un vecteur par un réel
6)vecteurs colinéaires
7) Vecteurs colinéaires et alignement
8) Relations entre deux vecteurs colinéaires
9)Milieu d'un segment

1) Définition

Un vecteur est un objet généralisant les notions géométries, de l’algèbre (segment de droite orienté) un vecteur est caractérisé par: sa direction, son sens et sa norme

exemple :

la direction de $\overrightarrow{u}$ est la droite (AB), le sens de $\overrightarrow{u}$ est de A vers B , la norme de $\overrightarrow{u}$ est la longueur de $AB =\sqrt{3^{2}+1^{2}}=\sqrt{10}=3,162$

2) Norme d'un vecteur :

la norme d'un vecteur $\overrightarrow{u}$correspond à sa mesure on la note

$\small \left \| \overrightarrow{u} \right \|$ , si $\small \overrightarrow{u}$ est un vecteur de coordonnées (x ; y ) alors $ \left \| \overrightarrow{u} \right \|=\sqrt{x^{2}+y^{2}}$

3)Egalité de deux vecteurs :

deux vecteurs sont égaux s'ils ont même direction , même sens et même norme ( même coordonnées)
Exemple:

les vecteurs $\small \overrightarrow{u}$et $\small \overrightarrow{v}$ ont le même sens et $\left \| \overrightarrow{AB} \right \|=\left \| \overrightarrow{CD} \right \|$

4)Somme de deux vecteurs :

si $ \overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs données , la somme de $ \overrightarrow{u} + \overrightarrow{v}$

on trace le vecteur $\overrightarrow{u}$ à partir d'une origine A ce qui donne le vecteur $\overrightarrow{AB}$ et en B on trace le vecteur $ \overrightarrow{v} $ce qui donne le vecteur $\overrightarrow{BC}$ et la somme des vecteurs $ \overrightarrow{u}$ et $ \overrightarrow{v}$ est le vecteur $\overrightarrow{AC}= \overrightarrow{u}+ \small \overrightarrow{v}$

Ou bien on applique règle du parallélogramme

$\overrightarrow{OA}+\overrightarrow{OB}= \overrightarrow{OM} =\overrightarrow{AC}$

Exemple:

5)Multiplication d'un vecteur par un réel :

Si $\overrightarrow{u}$ désigne un vecteur et $k$ un réel

le produit du vecteur $ \overrightarrow{u}$ par le réel $k$ est un (k \overrightarrow{u}\)

* si $k=0 ou \overrightarrow{u} =0 k \overrightarrow{u} =0$

** si $k >0 \ et\ \overrightarrow{u} ≠ 0$ $ k \overrightarrow{u} \ et \ \overrightarrow{u}$ ont la même direction, le même sens et $\left\| k\overrightarrow{u} \right\| =k\left\| \overrightarrow{u} \right\|$

***si $k < 0$ et $\overrightarrow{u}≠ 0$ alors $k \overrightarrow{u} et \overrightarrow{u}$ ont la même direction , sens opposés et $\left\| k\overrightarrow{u} \right\| =-k \overrightarrow{u}$

Exemple :soit $\overrightarrow{u}$ un vecteur donné et $\overrightarrow{v}$ et $ \overrightarrow{w}$ deux autres vecteurs tel que

$\overrightarrow{v} $ =$4 \overrightarrow{u}$ et $\overrightarrow{w}$ = $- 3 \overrightarrow{u}$

les ${\color{Red} {\overrightarrow{v}} } $et ${\color{Blue} {\overrightarrow{w}} }$ ont la même direction que celle de vecteur

$\overrightarrow{u}$,leurs droites sont parallèles

$\bg_white \small \overrightarrow{u}$ et $\bg_white {\color{Red} \overrightarrow{v} }$ sont le même sens car 4 > 0

$\bg_white \small \overrightarrow{u}$ et $\bg_white {\color{Blue} \overrightarrow{w} }$ sont de sens opposés car ( - 3) < 0

${\color{Red}{ \left\| \overrightarrow{v} \right\|}} =\left\| 4\overrightarrow{u} \right\|=4\left\| \overrightarrow{u} \right\|=4\sqrt{2²+1²}=4\sqrt{5}$=$\sqrt{(8)²+(4)²}=\sqrt{45}=3\sqrt{5}=\sqrt{4²(2²+1)}=4\sqrt{5}$

${\color{blue}{ \left\| \overrightarrow{w} \right\|}} =\left\| -3\overrightarrow{u}\right\|=3\left\| \overrightarrow{u} \right\|=4\sqrt{2²+1²}=3\sqrt{5}$$=\sqrt{(-6)²+(-3)²}=\sqrt{45}=3\sqrt{5}$

6)vecteurs colinéaires

définition :

on dit que deux vecteurs $\overrightarrow{u}$ et $\overrighatarrow{v}$ sont colinéaires s'il existe un réel $k$ tel que $\overrightarrow{v} =k\overrightarrow{v}$

Remarque :

le vecteur nul $\overrightarrow{0}$ est colinéaire à tout vecteur $\overrightarrow{u}$, car quel que soit $\overrightarrow{u} : 0 \overrightarrow{u}=\overrightarrow{0}$

$\overrightarrow{u} \neq0 \ et \overrightarrow{v} \neq0$sont colinéaire si et seulement si ils ont même direction

Exemples :

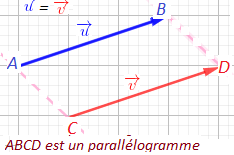
1) soit ABCD un parallélogramme et E un point donné tel que $\overrightarrow{ AE}=\frac{1}{4} \overrightarrow{AB}$

Montrer que$\overrightarrow{AE } \ et \ \overrightarrow{CD}$ sont colinéaires

Solution :

On a ABCD parallélogramme d'où $\overrightarrow{AB}=\overrightarrow{CD}$ donc $\overrightarrow{AE}=\frac{1}{4}\overrightarrow{DC}$ donc $\overrightarrow{AE}=-\frac{1}{4}\overrightarrow{CD}$ et donc on dit que $\overrightarrow{AE}\ et\ \overrightarrow{CD}$ sont colinéaires

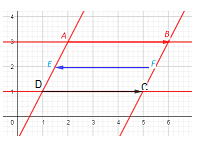
2) ABCD un parallélogramme et (EF) est parallèle à (AB) et (CD)

(AB)//(CD) donc $\overrightarrow{AB} \ et\ \overrightarrow{DC}$ sont colinéaire d'où il existe un réel $k$ tel que $\overrightarrow{AB} = k\overrightarrow{DC}$

$\overrightarrow{AB} \ et\ \overrightarrow{DC}$ sont de même sens alors $k > 0 \ et \ k=\frac{AB}{DC}$

(AB) // (FE) donc $\overrightarrow{AB}\ et\ \overrightarrow{FE}$ sont colinéaire d'où il existe un réel k' tel que $\overrightarrow{AB}=k' \overrightarrow{FE}$

$\overrightarrow{AB}\ et\ \overrightarrow{FE}$ sont de sens opposés donc $k' < 0 \ et \ k'=-\frac{AB}{FE}$

(FE) //( CD) donc $\overrightarrow{FE}\ et \ \overrightarrow{DC}$ sont colinéaires d'où il existe un réel $k''$ tel que $\overrightarrow{FE}=k''\overrightarrow{DC}$

$\overrightarrow{FE}\ et \ \overrightarrow{DC}$ sont de sens opposés donc $k'' < 0 \ et \ k''=-\frac{FE}{DC}$

7) Vecteurs colinéaires et alignement

On dit que trois point A , B et C sont alignés s'il existe un réel $k$ tel que $\overrightarrow{AB} =k \overrightarrow{AC} \ ou \ \overrightarrow{AB} =k \overrightarrow{BC}$

On dit que deux vecteurs :$\overrightarrow{u}\begin{pmatrix}x\\ y \end{pmatrix}\ et \ \overrightarrow{v}\begin{pmatrix}z\\ t \end{pmatrix}$ sont alignés si $det(\overrightarrow{u} ;\overrightarrow{v})=0\Leftrightarrow \begin{vmatrix}x \ \ t\\ y\ \ z \end{vmatrix}=xz-yt=0$

exemple:

Soient A et B deux point donnés placer le point C tel que $\overrightarrow{AC}=\frac{3}{4}\overrightarrow{AB}$

$\overrightarrow{AC}=\frac{3}{4}\overrightarrow{AB}$ donc par définition $\overrightarrow{AC}\ et \ \overrightarrow{AB}$ sont colinéaires d'où A , B et C sont alignés et de plus $\frac{3}{4}> 0$ donc $\overrightarrow{AC}\ et\ \overrightarrow{AB}$ sont de même sens et $AC=\frac{3}{4}AB$

8) Relations entre deux vecteurs colinéaires

Dans un plan muni d'un repère $\left (O;\overrightarrow{i} ; \overrightarrow{j}\right )$

deux vecteurs$\overrightarrow{u}$ et $\overrightarrow{v}$ ayant respectivement les coordonnées (x ; y ) et ( t ; z ) sont colinéaires si et seulement si x z = y t

c'est à dire déterminant $(\overrightarrow{u},\overrightarrow{v}) =\begin{vmatrix}x \ \ t\\ y\ \ z \end{vmatrix}=xz-yt=0$

Exemple:

Soit dans un repère du plan les vecteurs : $\overrightarrow{u}\begin{pmatrix} 3 \\ 1 \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} 6 \\ 2 \end{pmatrix}$

$\overrightarrow{u}\ et\ \overrightarrow{v}$ sont colinéaires car $(3\times 2)- (1\times 6)=6-6=0$

Soient $\overrightarrow{w}\begin{pmatrix}1\\ 3 \end{pmatrix}\ et\ \overrightarrow{m}\begin{pmatrix}2\\ 3 \end{pmatrix}$. les vecteurs : $\overrightarrow{w}\ et\ \overrightarrow{m}$ ne sont pas colinéaires car $det(\overrightarrow{u} ;\overrightarrow{v})\neq 0\Leftrightarrow \begin{vmatrix}1 \ \ 2\\ 3\ \ 3 \end{vmatrix}=1\times 3-3\times 2=-3$

8)Milieu d'un segment :

Définition

On dit que I est le milieu du segment [AB] si $\overrightarrow{IA}+ \overrightarrow{IB}=\overrightarrow{0}$

Propriété 1:

I milieu du segment [AB] si et seulement si

$\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}\\ \overrightarrow{IA}=-\overrightarrow{IB}=\overrightarrow{BI}\\ \overrightarrow{IB}=\frac{1}{2}\overrightarrow{AB}$

Propriété 2:

soit I milieu du segment [AB] il existe M un point du plan tel que :

$\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\ ou\ \frac{1}{2}(\overrightarrow{MA}+\overrightarrow{MB})=\overrightarrow{MI}$

Démonstration: $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}\\=2\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}\ or\ \overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$

Donc $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$

Propriété 3:

Soit ABC un triangle et I milieu de [AB] et J milieu de [AC]

montrer que: $\overrightarrow{IJ}=\frac{1}{2}\overrightarrow{BC}$

$\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{BJ}=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CJ}\\\\=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CA}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{CA})+\overrightarrow{BC}\\\\=\frac{1}{2}\overrightarrow{CB}+\overrightarrow{BC}=(1-\frac{1}{2})\overrightarrow{BC}=\frac{1}{2}\overrightarrow{BC}$

Soit ABC un triangle donné I Milieu de [AB] et J Milieu de [AC]

On a $\overrightarrow{IJ}=\frac{1}{2}\overrightarrow{BC}$ alors (I J) // (B C)

الرياضيات

القائمة الرئيسية

الصفحات