Parité dune fonction

 Fonctions paires :

Une fonction est dite paire si pour tout x dans son domaine, elle satisfait la condition suivante : 

$f(−x) =f(x)$

Cette fonction paire est symétrique par rapport à l'axe des ordonnées.

Exemple :

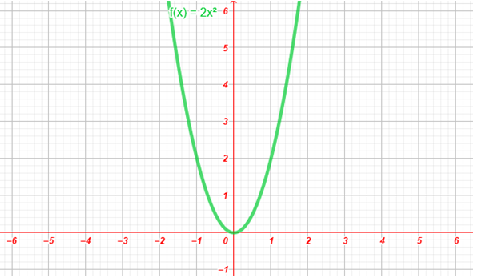
La fonction définie sur ℝ par` $f(x) =2x^2$ est paire car

  $$f(-x) =2(-x)^2=2x^2=f(x)$$

Sa courbe représentative est symétrique par rapport à l'axe des ordonnées comme le montre la figure ci-dessous 

Remarque si  $f(x) =(x-a)^n$ avec n est un entier pair

 

 La droite d’équation $x=a$ est un axe de symétrie de la courbe

 

 Représentative d’une fonction lorsque la condition suivante

  $f (a- x) =f (a+ x)$ est satisfait

 

Si $a=0$ on obtient :   $f(−x) =f(x)$

Exemple :

 $f(x) =(x-a)^2$    ($a=3$) a pour ensemble de définition l'ensemble des réels ℝ et aussi une fonction paire car :

 $f (3- x)$=$(3-x)-3)^{2}$

$=(3-x-3)^{2}=(-x)^{2}=x^{2}$ 

et  $f (3+ x)$=$(3+x)-3)^{2}$

$=(3+x-3)^{2}=(x)^{2}=x^{2}$ 

On voit que  $f (a- x) =f (a+ x)$=$x^{2}$ce qui montre que la fonction est symétrique par rapport à la droite d'équation 𝑥=3

Fonctions impaires

Une fonction est dite impaire si pour tout x dans son domaine, elle satisfait la condition suivante : 

$f(−x) =-f(x)$

Cette fonction impaire est symétrique par rapport à l'origine.

Exemple :

La fonction définie sur ℝ par` $f(x) =3x^3$ est impaire car :

  $$f(-x) =3(-x) ^3=-3x^3=-f(x)$$

Sa courbe représentative est symétrique par rapport à l'origine comme le montre la figure ci-dessous

Remarque : si $f(x) =(x-a)^n+b$ avec n est un entier impair

 

 Le point $M$ de coordonnées $(a;b)$ est centre de symétrie de 

  La courbe représentative d’une fonction lorsque la condition

 

 

 Suivante   $f (a+ x) + f(a-x) =2b$ est satisfait

 

Si (a ; b)= (0 ; 0)  on obtient   $f (0+ x) + f(0-x) =0$  donc $f(−x) =-f(x)$

 

Exemples : si $a\neq0$ et    $b\neq0$

 

Exemple 1:   $f(x) =(x-3)^5+1$

 

 $f(x) =(x-3)^5+1$ dans cette exemple ( $a=3$ et $b=1$)

 

Le domaine de définition de la fonction $f(x) =(x-3)^5+1$ est l'ensemble ℝ

 

Vérifiant $f (3+ x) + f(3-x) =2$

 

$f (3+ x)=((3+x)-3)^5+1$

$=(x)^5+1$

 

$f (3- x)=((3-x)-3)^5+1$

$=(-x)^5+1$

 

D’ou :

$f (3+ x) + f(3-x)  =(x)^5+1 - (x)^5+1=2$

$=2b$ car ($b=1$)

 

Le point $A$ de coordonnées $(3;1)$ est centre de symétrie de la courbe

 Représentative de la fonction$f(x) =(x+3)^5+1$ 

 

Car   $f (3+ x) + f(3-x) =2$ est satisfait  

اقرا ايضا Polynôme (division euclidienne) exercice corrigé

اقرا ايضا l'ensemble des réels

اقرا ايضاDévelopperA= (a+b)^{3}-(a-b)^{3}}

اقرا ايضاVecteurs

Exemple 2 :   $f(x)= \frac{(x-1)^3}{1-(x-1)^2}+2$

 

 $f(x)=\frac{(x-1)^3}{1-(x-1)^2}+2$ dans cette exemple ( $a=1 et b=2$)

 

Le domaine de définition de la fonction   $f(x)=\frac{(x-1)^3}{1-(x-1)^2}+2$   est en fait

   

$D= \left\{ x ∈ ℝ / 1 – (x-1)^2\ \neq  0  \right\}$ 

  Le dénominateur     $1 -(1- x)^2$ doit être différent de zéro.

 

Résoudre :  $1 -(1- x)^2 \neq 0$ ce qui donne

    $1 -(1- 2x+x^2) \neq 0$ $\implies 2x-x^2 \neq 0$

                         $\implies x(2-x) \neq 0$

                           $\implies 2-x \neq0$ et $x \neq 0$

                 donc $x \neq2$ et $x \neq 0$

Donc D = ℝ – {0, 2}

 

Le centre de symétrie de la courbe représentative de cette fonction 

 

 

$f(x)=\frac{(x-1)^3}{1-(x-1)^2}+2$

 

Est le point $M (1,2)$   car    $f (1+ x) + f(1-x) =4$

Calculons donc $f (1+ x) + f(1-x)$

 

=[ $\frac{(1+x-1)^3}{1 - (1+x-1)^2} + 2$ ]+[ $\frac{(1-x-1)^3}{1 - (1-x-1)^2} + 2$]

 

 

=[ $\frac{x^3}{1 - x^2} + 2$ ]+[ $\frac{-x^3}{1 - x^2} + 2$]

 

 

 = ($\frac{x^3}{1 - x^2}$ )+ ($\frac{-x^3}{1 - x^2}$)+$2+2$

 

=$\frac{x^3}{1 - x^2}   )- ( \frac{x^3}{1 - x^2}  )+4$

$= 0+4=4= 2b \ (b=2)$

 

Ce qui montre que le centre de symétrie de la fonction \

$f(x)=\frac{(x-1)^3}{1-(x-1)^2}+2$  est le point $M (1,2)$ et

 Présente des asymptotes verticales aux points $x=0$ et $x=2$ comme le montre le graphe de la fonction

pdf à télécharger