2) Démonstration par la contraposée
p⇒ q ⇔ ¬ p∨ q ⇔ ¬q⇒ ¬p
Pour démontrer p ⇒ q par contra position revient à démontrer la contraposée de ¬q⇒ ¬p c'est à dire on suppose que q est fausse et en déduit que p est fausse
Exemple:
Démontrons que ( ∀ x∈ ℝ+):(x≠ 4⇒ 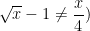
On suppose que 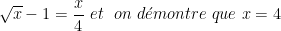
et en enfin : ( ∀ x∈ ℝ+):(x≠ 4⇒ 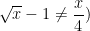


Commentaires
Enregistrer un commentaire